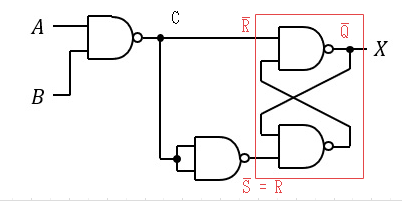
$$$$

赤い部分はRSフリップフロップ回路。NAND回路で作成しているのでNOR回路の入出力は反転している。論理回路参照。 $$$$

$$\overline{R}$$ $$\overline{S}$$ $$\overline{Q^{n+1}}$$

0 0 不定

0 1 1

1 0 0

1 1 $$\overline{Q^n}$$
$$\overline{A \cdot B} =C, フリップフロップ回路の入力(\overline{R},\overline{S})は (0,1)(1,0)のみ。$$

A B $$C =\overline{R}$$ $$X = \overline{Q}$$

0 0 1 0

0 1 1 0

1 0 1 0

1 1 0 1
Ans.(3)

$$\overline{R}$$	$$\overline{S}$$	$$\overline{Q^{n+1}}$$
0	0	不定
0	1	1
1	0	0
1	1	$$\overline{Q^n}$$

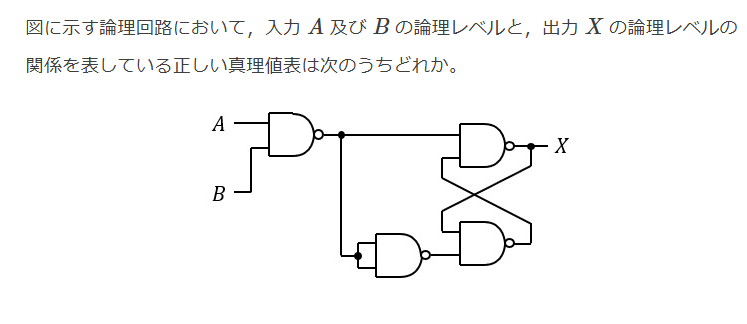
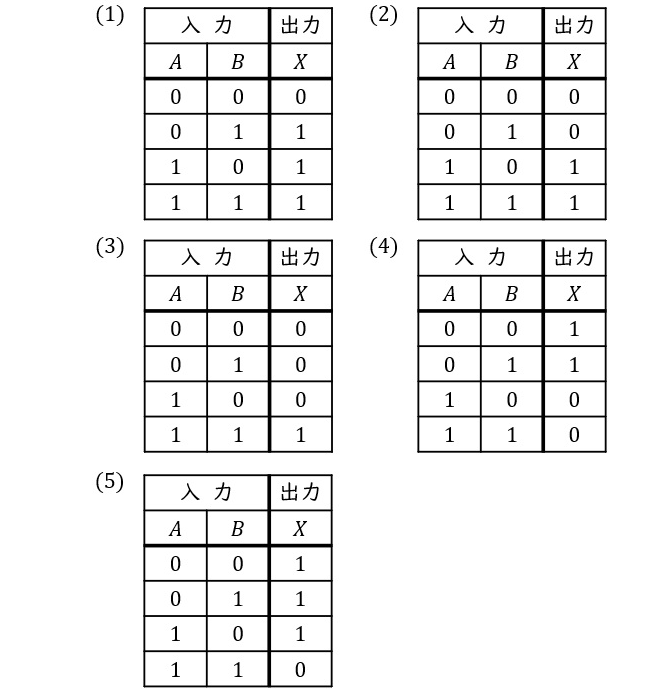
A	B	$$C =\overline{R}$$	$$X = \overline{Q}$$
0	0	1	0
0	1	1	0
1	0	1	0
1	1	0	1

各ビットごとの演算。論理演算参照

$$A \cdot B = (1000 0001)_2$$ $$A + B = (1110 0111)_2$$ $$A \oplus B = (0110 0110)_2$$ $$\overline{A \cdot B} = (0111 1110)_2$$

２進数を１６進数に変換する。n進数の基礎参照

Ans.(2)

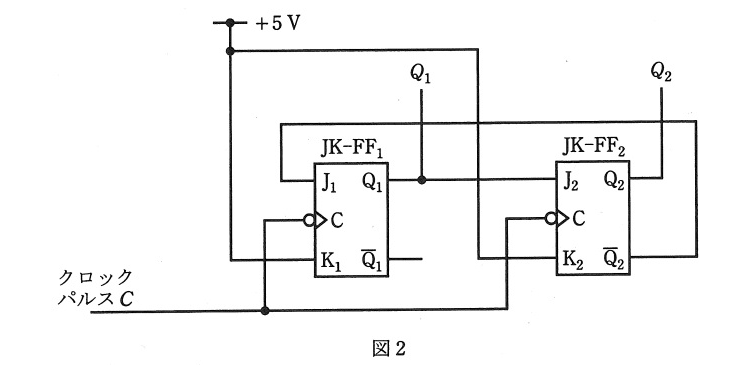
(a)

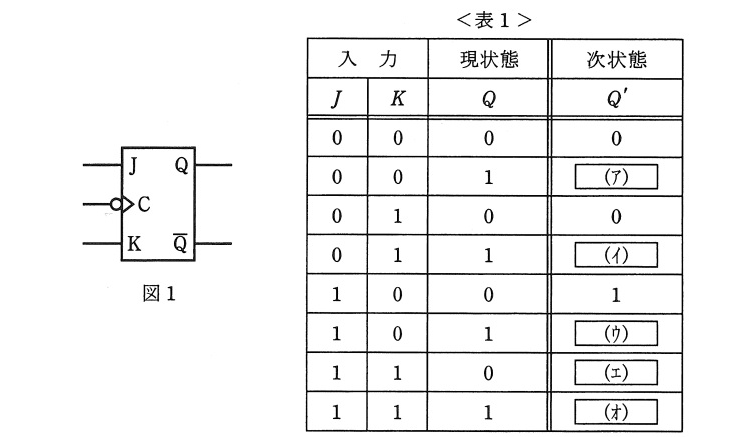
J-KフリップフロップにはJとKの二つの入力、QとQ（Qの否定）の二つの出力を持つ。

Jⁿ	Kⁿ	Qⁿ⁺¹
0	0	Qⁿ
0	1	1
1	0	0
1	1	Qⁿ

Ans.(4)

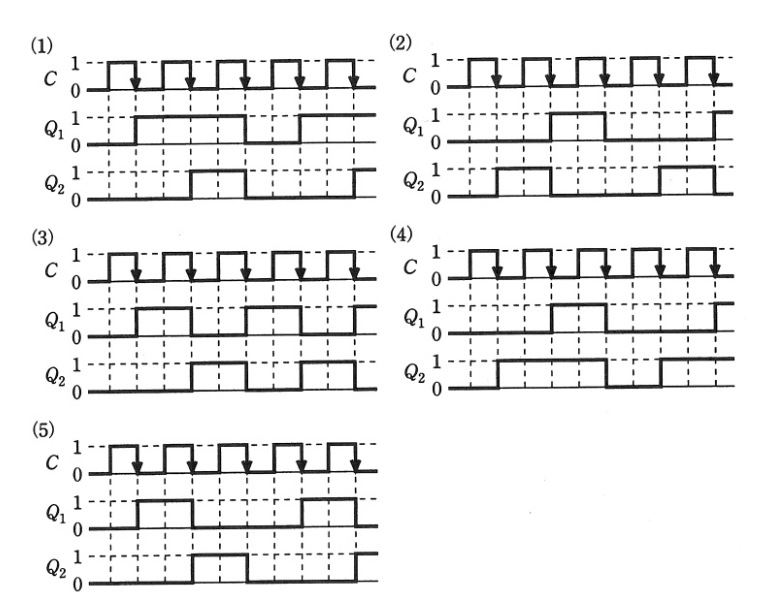
(b)

クロックパルスの立下り↓で出力が変化する。

Ans.(5)

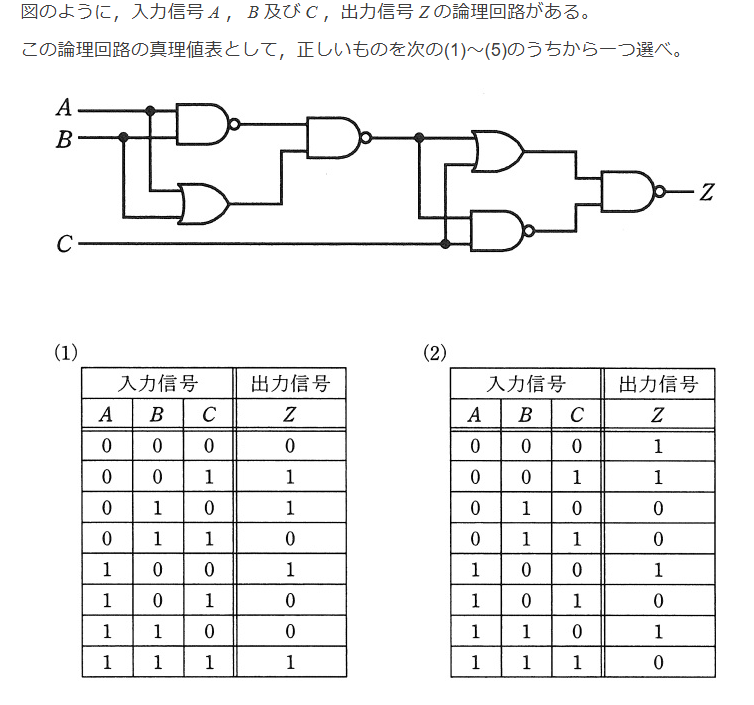
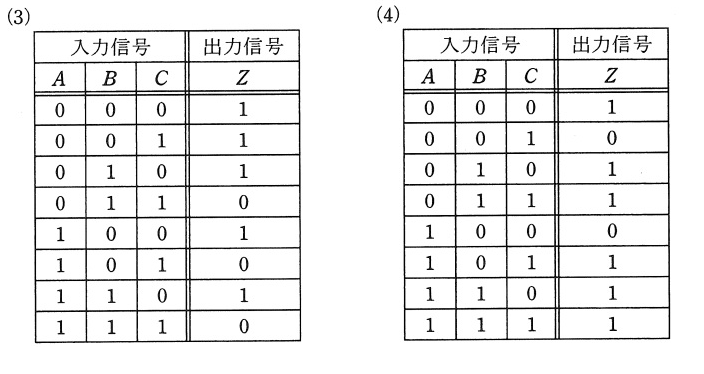
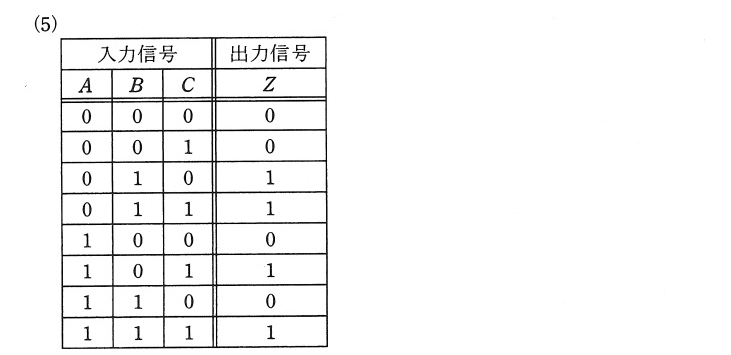
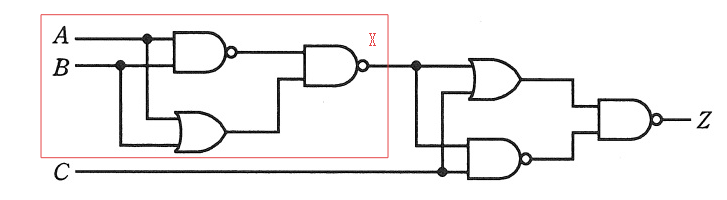
入力A,B　出力X　と、入力X,C　出力Zの回路に分けて考えてみる。

$$A$$	$$B$$	$$X$$
0	0	1
0	1	0
1	0	0
1	1	1

$$X$$	$$C$$	$$Z$$
0	0	1
0	1	0
1	0	0
1	1	1

二つの真理値表を合わせる。例えばA=0,B=0,C=0の時は、A=0,B=0でXは1、X=1,C=0でZ=0。

$$A$$	$$B$$	X	C	$$Z$$
0	0	1	0	0
0	0	1	1	1
0	1	0	0	1
0	1	0	1	0
1	0	0	0	1
1	0	0	1	0
1	1	1	0	0
1	1	1	1	1

Ans.(1)

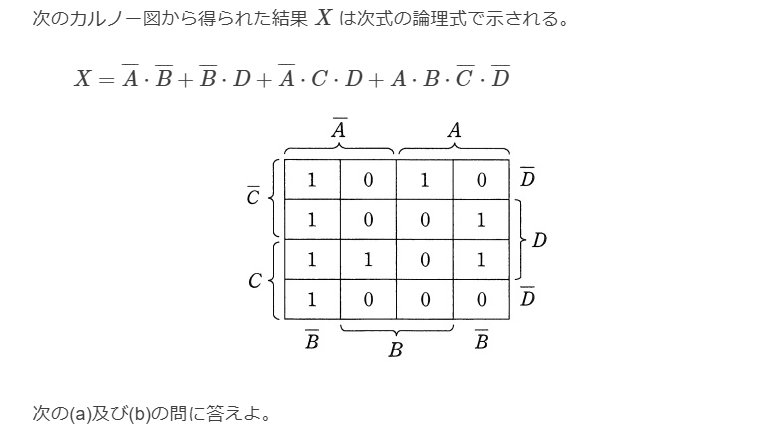
ド・モルガンの定理を使用。論理演算参照

$$\overline{A+B} = \overline{A} \cdot \overline{B},\overline{A \cdot B} = \overline{A} + \overline{B}$$ (a)$$NANDのみの場合は\overline{A+B} = \overline{A} \cdot \overline{B}$$

を使ってORをANDに変換する。論理回路参照。

$$X' = \overline{\overline{X'}} = \overline{\overline{\overline A \cdot \overline B+\overline B \cdot D }}$$ $$= \overline{(\overline{\overline A \cdot \overline B})) \cdot (\overline{\overline B \cdot D })}$$ Ans.(5) (b)$$NORのみの場合は\overline{A \cdot B} = \overline{A} + \overline{B}を使って$$

ANDをORに変換する

$$\overline{\overline{\overline A \cdot \overline B}} = \overline{\overline{\overline A} + \overline{\overline B}} = \overline{ A \cdot B} $$ $$\overline A \cdot \overline B+\overline B \cdot D = (\overline{ A + B}) + (\overline{ B + \overline D})$$ $$出力が否定の形になってないので、二重否定する$$ $$= \overline{\overline{(\overline{ A + B}) + (\overline{ B + \overline D})}}$$ $$$$ Ans.(3)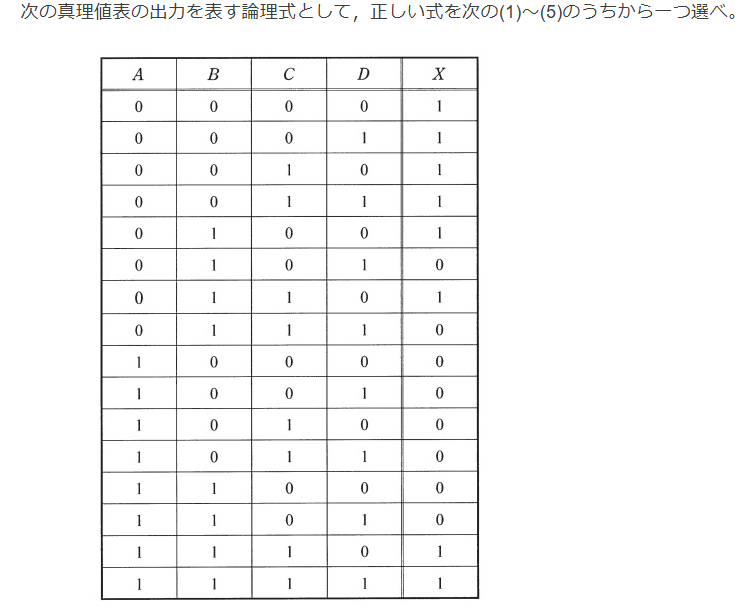

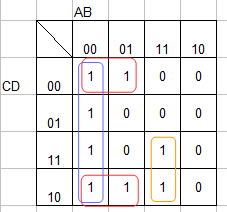
カルノー図を使って論理式を簡略化する。論理演算参照。カルノー図で隣り合う（２つ・４つ・８つ等）論理式は簡略化できる。
$$青枠の４つはCDがどの値でもXは１なので、\overline A \cdot \overline B$$ $$橙枠の２つはDがどの値でも１なので、A \cdot B \cdot C$$ $$赤枠の４つはBCがどの値でも１なので、\overline A \cdot \overline D$$ Ans.(3)