直流機

直流機は外側で静止している界磁と内側で回転する電機子に分けられる。直流電力を加えると電動機として働き動力を得る。外部から動力を加えると発電機として働き電力を得る。

励起

励起とは界磁コイルに電流を流して主磁束Φを発生させること。

他励：界磁コイルが直流発電機と別の回路。

分巻：直流発電機の電機子と界磁コイルが並列に接続されている回路

直巻：直流発電機の電機子と界磁コイルが直列に接続されている回路

複巻：直流発電機の電機子と界磁コイルが並列と直列に接続されている回路

直巻発電機は発電機の電機子と界磁コイルが直列に接続されているので、負荷を接続しないと界磁電流が流れず電圧の確立がされない。
他励発電機は界磁コイルが直流発電機と別の回路なので電圧の確立はできいる
分巻発電機は発電機の電機子と界磁コイルが並列に接続されているので端子電圧が減ると界磁電流も減るので負荷による変動が大きい。残留磁気に対して分巻巻線の起磁力の向きが逆になる接続だと電圧の確立ができない
Ans.(2)

Ans.(4)

直巻電動機のトルクは電流の二乗に比例する
Ans.(3)

Ans.(4)

直流発電機の誘導起電力

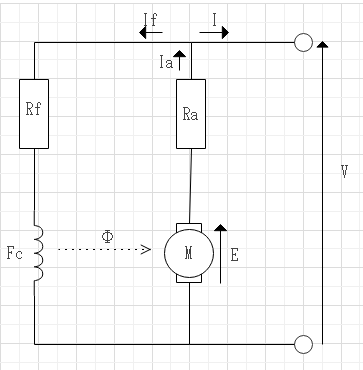
$$E = (\frac{PZ}{60a})\Phi N$$

$$E = V + I_a R_a$$

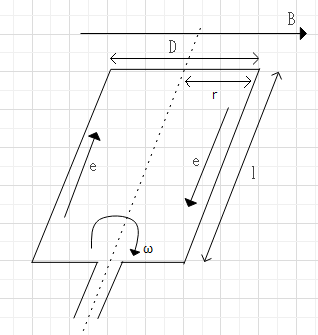
$$e = v B l$$

$$v = r \omega = \frac{D}{2}\frac{2\pi N}{60} = \frac{\pi D N}{60}$$

$$B = \frac{P \Phi}{\pi D l},e = \frac{P \Phi N}{60}$$

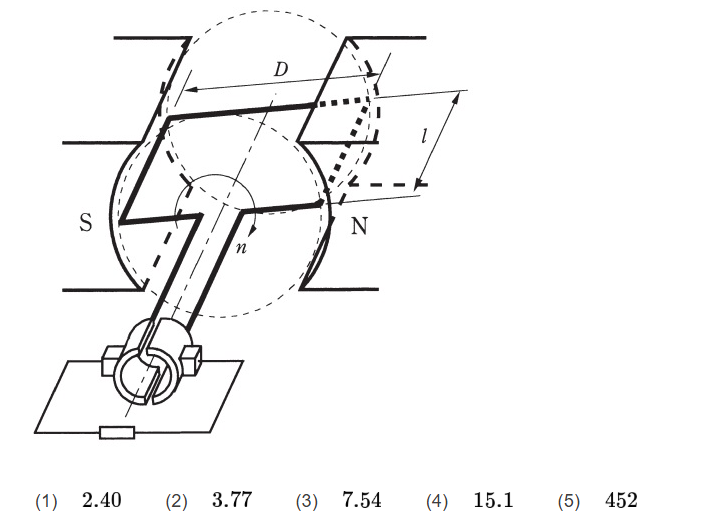
$$e =n v B l,v = \frac{\pi D N}{60}.n:磁極数$$ $$e = 2\frac{\pi\times 0.5 \times 1200}{60}0.4 \times 0.3$$ $$= 7.54[V]$$ $$$$ $$$$ Ans.(3)

Ans.(1)

分巻発電機なので電機子と界磁コイルが並列に接続されている。
$$定格効率＝\frac{定格出力}{定格出力＋固定損＋直接負荷損＋界磁回路損}$$ 固定損：鉄損や機械損 直接負荷損：電機子の抵抗損 界磁回路損：界磁の抵抗損 漂遊負荷損：発生箇所不明の損失。 $$定格電流＝\frac{50 \times 10^3}{200} = 250[A]$$ $$界磁電流＝\frac{200}{200} = 1[A] $$ $$電機子電流＝250+1 = 251[A]$$ $$定格効率0.94 = \frac{50 \times 10^3}{50 \times 10^3＋固定損＋0.03 \times 251^2＋200 \times 1^2}$$ $$固定損＝1.10[kW]$$ $$$$ $$$$ $$$$ $$$$ Ans.(1)

直流電動機

$$逆起電力:E = (\frac{P Z}{60 a})\Phi N$$

$$トルク：T =T (\frac{P Z}{2 \pi a})\Phi I_a = \frac{P}{\omega }$$

$$出力:P = E I_a = \frac{2 \pi a T}{P Z \Phi}$$

$$E = V - I_a R_a$$ $$N = (\frac{60 a}{P Z})\frac{V - I_a R_a}{\Phi }$$

$$P = E I_a$$ $$逆起電力=\frac{5 \times 10^3}{23.6} = 211.9[V]$$ $$E = V - I_a R_a, V = E + I_a R_a$$ $$220 = 211.9 + 23.6 \times R_a$$ $$R_a = 0.343$$ $$電機子電流20Aのときの逆起電力は$$ $$E=220 - 20 \times 0.343 = 213$$ $$$$ Ans.(3)

$$E = V - I_a R_a$$ $$入力電圧110Vの時の逆起電力=110-50 \times 0.20 = 100[V]$$ $$入力電圧80V、電流変化なしの時の逆起電力=80-50 \times 0.20 = 70[V]$$ $$E = (\frac{P Z}{60 a})\Phi N　より$$ $$逆起電力と回転数は比例する。逆起電力70Vの時の回転数は$$ $$N=\farc{70}{100}1200 = 840[min^{-1}]$$ Ans.(2)

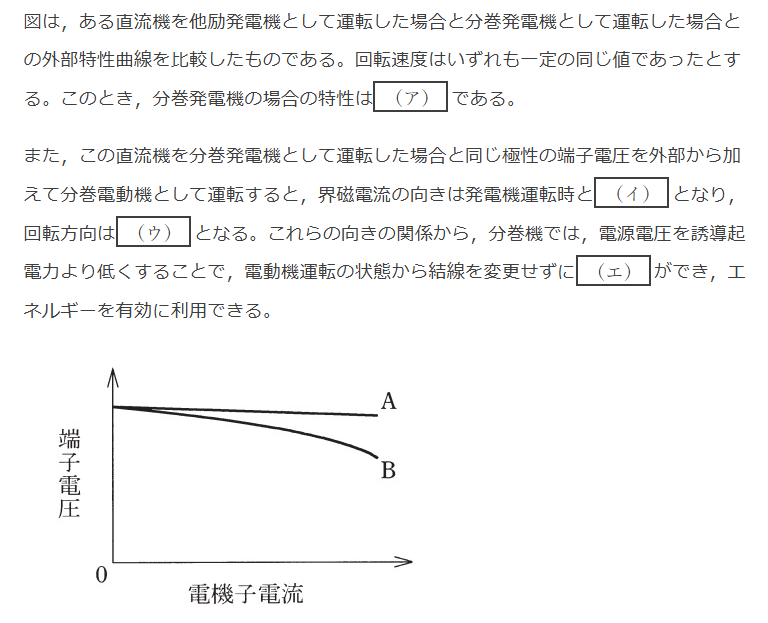
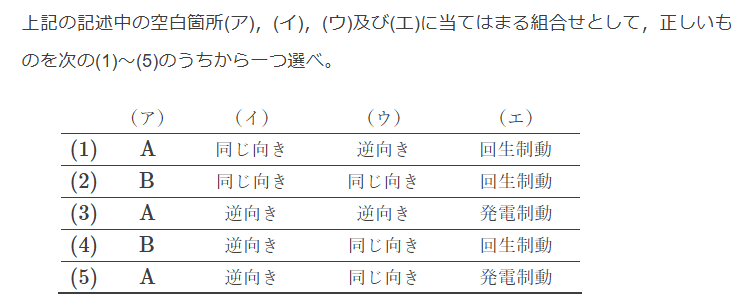
Ans.(2)