論理回路とは論理演算を行うための回路のこと。組み合わせ回路、順序回路などがある。
論理式
論理演算：真と偽の二つの元（真理値）だけを持つ集合における演算。
真理値表：変数の全ての組み合わせについてどのような論理値になるか示した表。
論理式：論理変数と論理記号をある規則に従って並べた記号の列。
ブール代数（論理代数）：二つの値（０と１）と三つの基本演算（AND OR NOT）で論理式を表す。
０…偽、１…真。AND…論理積,・、OR…論理和,＋、NOT…否定,A
真理値表
| A | B | AND | OR | NAND | NOR | XNOR |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
論理演算と論理素子
正論理：論理回路の信号がある場合（H）を１（真）、ない場合（L）を０（偽）とする。
負論理：信号がある場合（H）を０（偽）、ない場合（L）を１（真）とする。
例を挙げると、AND素子を入出力ともに負論理で使用するとOR機能として働く。
論理回路をNAND素子（NOR素子）だけで作成した場合に正論理・負論理がわかっていると理解しやすい。NAND素子によって出力が反転されている場合にはそれが入力される場合には負論理として考えればいい。
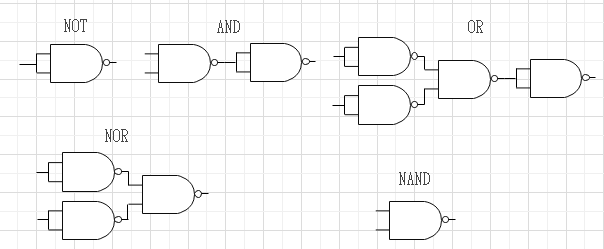
NANDやNOR素子だけですべての（AND,OR,NOT,NAND,NOR）機能を表現できる。これらの素子には完備性がある。
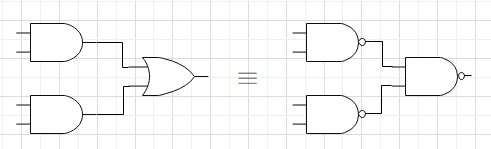
XY+YZのような論理関数だとNAND素子だけで簡単に置き換えられる。
組み合わせ回路
組み合わせ回路：出力がその時の入力のみによって決まる回路。真理値表やブール代数で表すことができる。
組み合わせ回路を真理値表やブール代数で表現し、その論理関数を簡単化する。
半加算器
入力が二つの二進数一桁の数（A,B）、出力が二進数一桁の和（S）と上位への桁上げの値（C）を表す半加算器を設計する。
真理値表は以下の通り。
| A | B | C | S | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
出力の論理関数は $$C = AB$$ $$S = \overline A B + A\overline B = A \oplus B \oplus は排他的論理和（XOR）$$
これ以上簡単化できないので、このまま論理回路を作成する。
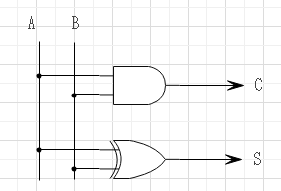
全加算器
入力が二つの二進数一桁の数（A,B）のほかに下位の桁からの桁上げの数（C'）、出力が二進数一桁の和（S）と上位への桁上げの値（C）を表す全加算器を設計する。
真理値表は以下の通り。
| A | B | C' | C | S | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 |
出力の論理関数は $$C = \overline A \overline B{C'} + \overline A B \overline{C'} + A \overline B \overline{C'} + AB{C'}$$ $$S = \overline AB{C'} + A \overline B{C'} + AB \overline {C'} + AB{C'}$$
カルノー図を用いて簡単化する。
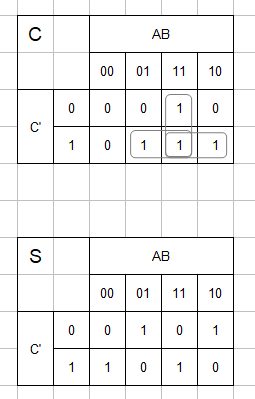
出力Cのみ簡単化できて、 $$C = AB + BC' + AC'$$
また $$ A \oplus B = \overline A B + A \overline B, \overline {A \oplus B} = AB + \overline A \overline B$$を用いるとSも変形できて $$S = (A \oplus B) \overline {C'} + \overline {(A \oplus B)} C' = (A \oplus B) \oplus C'$$ これらを用いて論理回路を作成する。
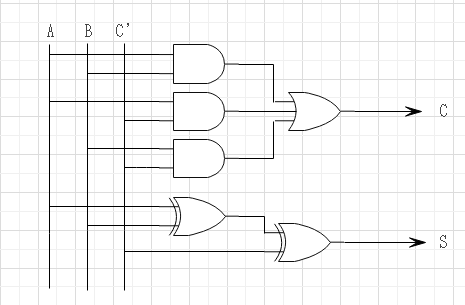
順序回路
ある時刻における出力がその時点での入力と回路の状態によって定まる。順序回路＝組み合わせ回路＋記憶素子。
記憶素子にはフリップフロップがある。
R-Sフリップフロップ
R-SフリップフロップにはRとSの二つの入力、QとQ（Qの否定）の二つの出力を持つ。フリップフロップにはほかに初期状態にするためのクリア・プリセット入力、同期用のクロック入力がある。クロックパルスのタイミングで出力が変化する。
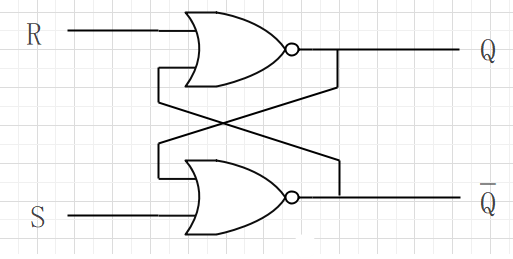
特性方程式
特性表：入力と出力、状態の関係を示した表。
| 時刻ｎ | 時刻（ｎ＋１） | |
|---|---|---|
| Rn | Sn | Qn+1 |
| 0 | 0 | Qn |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 不定 |
特性方程式：時刻ｎにおける入力および状態によって、時刻（ｎ＋１）の状態を定義する方程式。
特性方程式は特性表（の簡単化）から作成する。
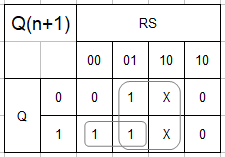
R-Sフリップフロップの特性方程式 $$Q^{n+1} = (S + \overline R Q )^n$$ $$(RS)^n = 0$$ R = 1,S = 1の時は出力が不定のため入力を組み合わせ禁止（RS = 0）とする。
入力方程式
応用方程式：いくつかのフリップフロップの状態を決定する論理関数。 $$Q^{n+1} = (g_1 Q + g_2 \overline Q )^n$$
入力方程式：応用方程式からフリップフロップの各入力を求めた方程式
特性方程式を応用方程式に代入。 S + \overline R Q = g_1 Q + g_2 \overline Q、RS = 0$$
| g1 | g2 | Q | S+RQ | R | S |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | a0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | a4 | 0 |
| 1 | 0 | 1 | 1 | 0 | a5 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | a7 |
aXは0でも１でもいい任意定数。
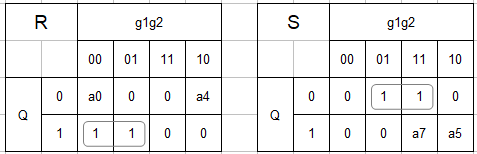$$R = \overline {g_1} Q , S = g_2 \overline Q$$
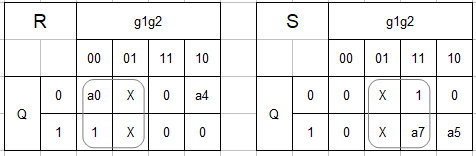$$ \overline {g_1}g_2 = 0(組み合わせ禁止)とすると、 $$
$$R = \overline {g_1} , S = g_2 となる。$$
状態遷移図
状態遷移図：状態を円で示し、状態の遷移を矢印で示した図。その時の入力と出力を（入力／出力）で示す。
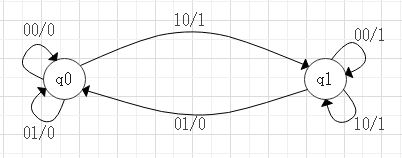
q0:出力０の状態。q1:出力１の状態。00/0:R、Sの入力／出力Q
遷移表
| 時刻ｎの状態 | （ｎ＋１）の状態 | 出力Q | ||||||
|---|---|---|---|---|---|---|---|---|
| 00 | 01 | 10 | 11 | 00 | 01 | 10 | 11 | |
| q0 | q0 | q0 | q1 | - | 0 | 0 | 1 | - |
| q1 | q1 | q0 | q1 | - | 1 | 0 | 1 | - |
Tフリップフロップ
TフリップフロップにはTの一つの入力、QとQ（Qの否定）の二つの出力を持つ。
| Tn | Qn+1 |
|---|---|
| 0 | Qn |
| 1 | Qn |
Tフリップフロップの特性方程式 $$Q^{n+1} = (\overline T Q + T \overline Q )^n$$
J-Kフリップフロップ
J-KフリップフロップにはJとKの二つの入力、QとQ（Qの否定）の二つの出力を持つ。
| Jn | Kn | Qn+1 |
|---|---|---|
| 0 | 0 | Qn |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | Qn |
J-Kフリップフロップの特性方程式 $$Q^{n+1} = (\overline K Q + J \overline Q )^n$$
Dフリップフロップ
DフリップフロップにはDの一つの入力、QとQ（Qの否定）の二つの出力を持つ。
| Dn | Qn+1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Tフリップフロップの特性方程式 $$Q^{n+1} = D^n$$ クロックパルスCのタイミングで出力が変化するので、 $$Q^{n+1} = C D^n + \overline C Q^n$$
順序回路の設計
状態遷移図・遷移表→状態の簡単化→状態の割り当て→応用方程式→入力方程式→回路生成
状態の簡単化
等価な状態（同じ入力と出力の組み合わせ）をまとめて一つにすることで状態数を減少させる。
１．すべての入力のそれぞれに対して同じ出力を与える状態を一つにまとめる。まとめた中で各入力に対してその次の状態も同じなら、一つの状態にまとめ新しい遷移表を作る。
２．新しい遷移表の各組の状態を新しく置き換える。一つの組の中に等価な状態がなければ、これが別の組になるように分け、新しい遷移表を作る。
３．すべての組が一つの状態か等価ないくつかの状態のみを含むなら、あたらめて状態を割り当てる。
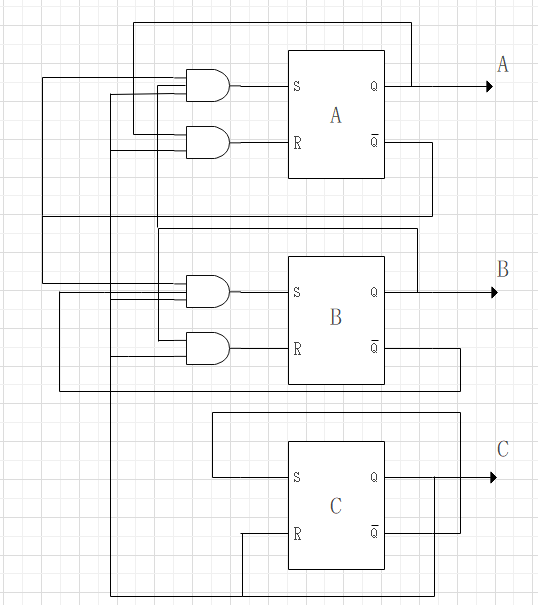
６進カウンターの設計
クロックごとに０から５まで１ずつ増えるカウンター。５の次は０に戻る。今回はR-Sフリップフロップを用いたカウンタを説明する。
遷移表
| 時刻ｎの状態 | 時刻ｎ | 時刻（ｎ＋１） | ||||
|---|---|---|---|---|---|---|
| Ａ | Ｂ | Ｃ | Ａ | Ｂ | Ｃ | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 1 | 1 |
| 3 | 0 | 1 | 1 | 1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 1 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 | 0 | 0 |
| 6 | 1 | 1 | 0 | X | X | X |
| 7 | 1 | 1 | 1 | X | X | X |
状態６，７は存在しない。なのでABC,ABCは組み合わせ禁止（AB=0）。出力がすべて違うので状態の簡単化はできない。状態の割り当てもそのまま（０〜５）。状態数が６なのでフリックプロップの数は３（A,B,C）
応用方程式
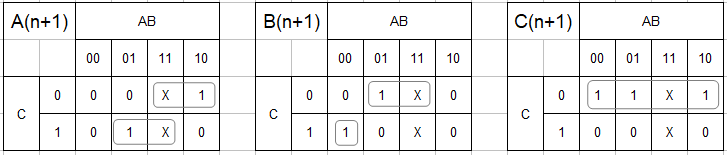$$A^{n+1} = (A \overline C + BC)^n,B^{n+1} = (B \overline C + \overline A \overline B C )^n,C^{n+1} = (\overline C )^n$$
入力方程式
R-Sフリップフロップの入力方程式
$$ \left\{ \begin{array}{l} R = \overline {g_1} Q \\ S = g_2 \overline Q \end{array} \right. $$応用方程式
$$Q^{n+1} = (g_1 Q + g_2 \overline Q )^n$$
を用いて入力方程式を導き出す。
$$ \left\{ \begin{array}{l} A^{n+1} = (\overline C A + (ABC=0) +BC \overline A)^n\\ B^{n+1} = (\overline C B + \overline A C \overline B)^n\\ C^{n+1} = (0・C + 1 ・ \overline C )^n \end{array} \right. $$ $$ \left\{ \begin{array}{l} R_A = AC \\ S_A = \overline ABC \end{array} \right. \left\{ \begin{array}{l} R_B = BC\\ S_B = \overline A \overline B C \end{array} \right. \left\{ \begin{array}{l} R_C = C\\ S_C = \overline C \end{array} \right. $$入力方程式から回路を作成する。 $$フリップフロップの入力R：R_A,R_B,R_C.入力S:S_A,S_B,S_C$$ $$出力Q:A,B,C$$に対応。
