フィードバック制御
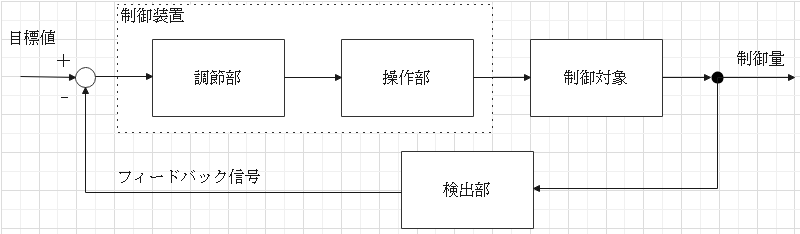
ブロック線図 伝達関数
伝達関数G(s)
$$G(s) = \frac{出力をラプラス変換した値}{入力をラプラス変換した値} = \frac{X(s)}{U(s)}$$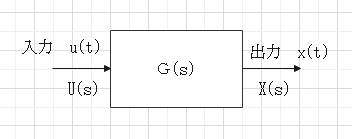
直列結合
並列結合
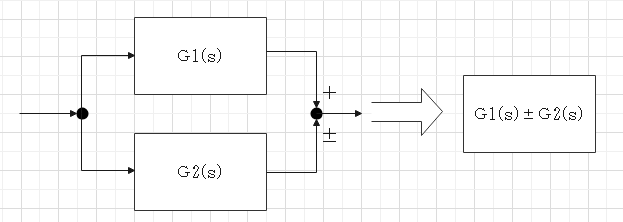
フィードバック結合
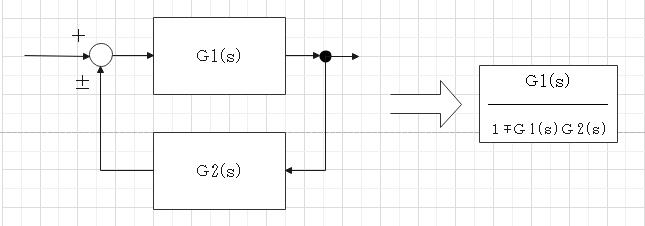
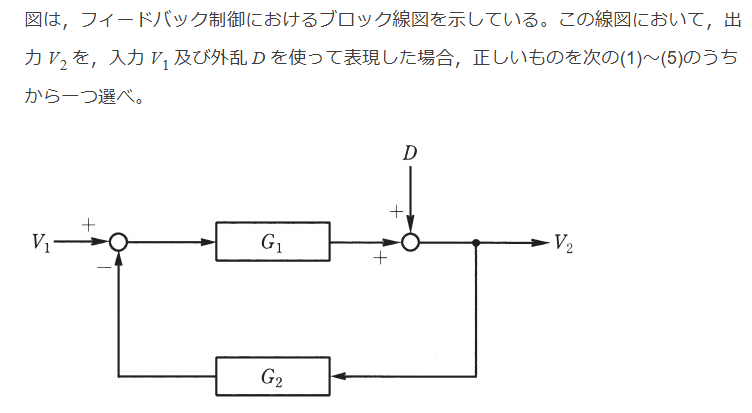
$$V_2 = G_1 (V_1 - G_2 V_2) + D$$ $$(1 + G_1 G_2)V_2 = G_1 V_1 +D$$ $$V_2 = \frac{G_1 V_1 + D}{1 + G_1 G_2 }$$ $$$$ Ans.(5)
ラプラス変換
実数ｔの関数を複素数ｓの関数に変換
$$ \cal{L} [ f(t) ] = F(s) = \int_{0}^{\infty} f(t) e^{-st} dt$$制御分野では時間領域（ｔ）の関数を周波数領域（ｊω）に関数に変換するのによく使われる。
微分のラプラス変換
$$ \cal{L} [ \frac{d f(t)}{dt} ] =sF(s)-f(0)$$初期値f(0)=0ならば、微分がｓの積に変わる。
積分のラプラス変換
$$ \cal{L} [ \int f(t)dt ] = \frac{1}{s}F(s) + \frac{f^{(-1)}(0)}{s}$$初期値f(-1)(0)=0ならば積分が１／ｓの積に変わる
$$$$PID制御
フィードバック制御にて出力値と目標値との偏差に制御装置で比例・積分・微分動作を加えることで出力値の制御する方法。
$$比例動作（P動作） x(t) = Kp・u(t)$$ $$積分動作（I動作） x(t) = \frac{1}{T_I} \int u(t)$$ $$微分動作（D動作） x(t) = T_D \frac{d u(t)}{dt}$$ $$PID動作 x(t) = Kp（\frac{1}{T_I} \int u(t) + T_D \frac{d u(t)}{dt}）$$ $$$$ $$$$ $$P制御：調節器の伝達関数 K_p$$オフセット（制御結果と目標値との偏差、定常偏差）が生じる。
$$PI制御：調節器の伝達関数 K_p(1 + \frac{1}{T_I s})$$オフセットを０にする。TI:積分時間（入力に一定の信号が与えられたときにP動作によるものとI動作によるものとが等しくなる時間）。積分時間が小さいほど早くオフセットの矯正が行われるが、オーバーシュートや出力値が振動する現象が起きやすくなる。急激な変化には対応できない。
$$PID制御：調節器の伝達関数 K_p(1 + \frac{1}{T_I s }+ T_D s)$$TD:微分時間（入力に速度入力信号（一定の変化量を持つ信号）を与えられたときにP動作によるものとD動作によるものとが等しくなる時間）微分時間が大きいほど変動に追従できるが、制御が不安定になりやすくなる。
シーケンス制御
あらかじめ定められた順序または手続きに従って制御の各段階を逐次進めていく制御
(3)はフィードバック制御
Ans.(3)
周波数応答特性
正弦波状入力に対する要素の定常応答。
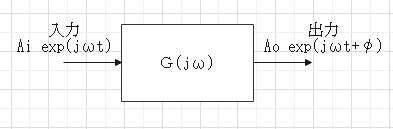$$振幅比（ゲイン）： \frac{A_o}{A_i} = |G(j \omega)| = \sqrt{Re(\omega)^2 + Im(\omega)^2}$$
$$位相ずれ \varphi = \angle G(j \omega) = \arctan{\frac{Im(\omega)}{Re(\omega)}}$$
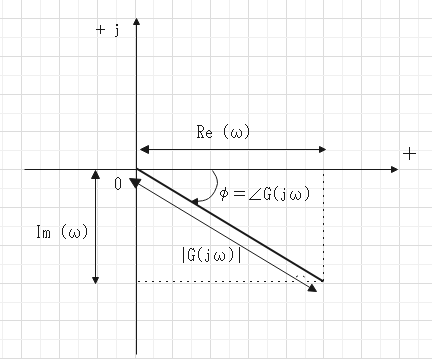
ベクトル軌跡
ωを０から∞まで変化させたときのベクトルの先端が描く軌跡
一次遅れ要素
$$G(s) = \frac{1}{1+Ts} | $$$$G(j \omega)| = \frac{1}{\sqrt{1 + (\omega T)^2}}\angle G(j \omega) = \arctan{(-\omega T)} $$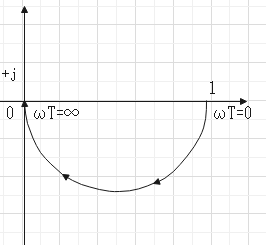
積分要素
$$G(s) = \frac{1}{T s}$$$$ G(j \omega) = - \frac{j}{\omega T}$$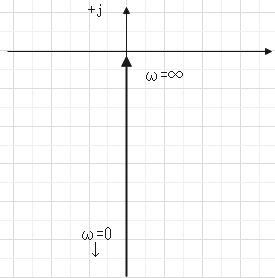
微分要素
$$G(s) = sT $$$$G(j \omega) = j\omega T$$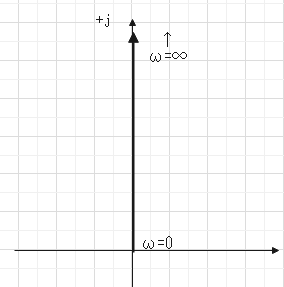
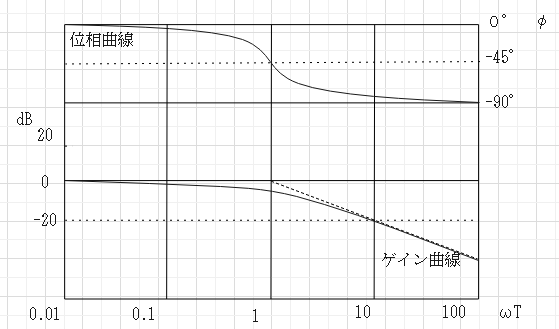
Bode線図
角周波数ωを横軸（対数目盛）、ゲインの対数20log10|G(jω)|(単位dB)と位相ずれ（deg）を縦軸にとって周波数特定を示した線図
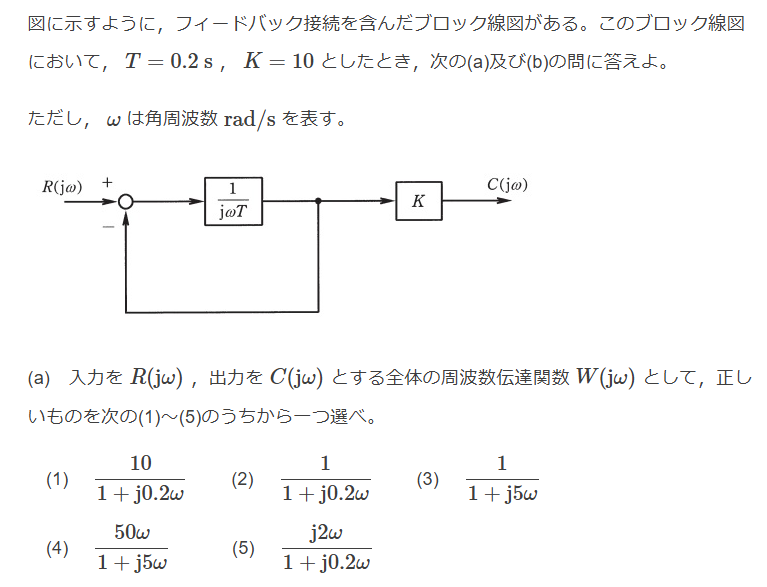
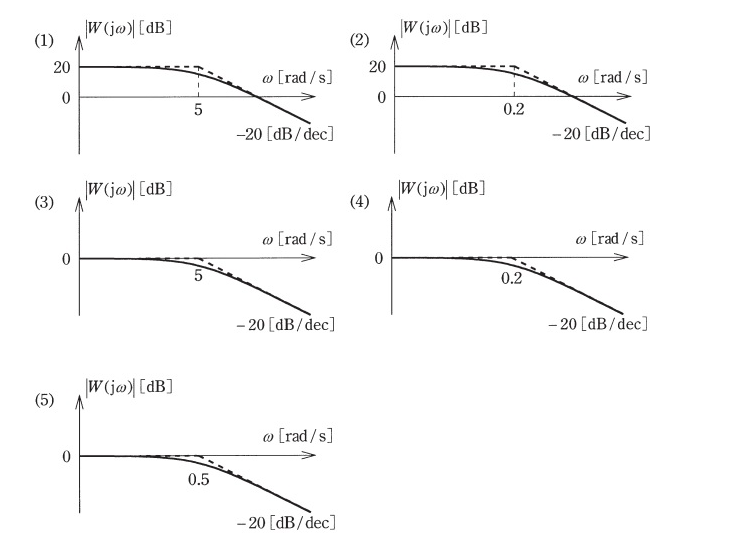
(a)
$$W(j \omega) = K \frac{\frac{1}{j \omega T}}{1+ \frac{1}{j \omega T}} = \frac{K}{j \omega T +1}$$
$$= \frac{10}{1 + j 0.2 \omega}$$
Ans.(1)
(b)
$$|W(j \omega)| = \frac{10}{\root \of {1 + (0.2 \omega )^2}}$$
$$ゲイン 20 log_{10}|W(j \omega)|$$
$$\omega = 0 の時 ゲインは20 log_{10}(\frac{10}{\root \of {1 + (0.2 \omega )^2}}) = 20[dB]$$
$$折れ点角周波数：|W(j 0)|に対し\frac{1}{\root \of 2} 倍になる角周波数$$
$$|W(j \omega)| = \frac{10}{\root \of {1 + (0.2 \omega )^2}} = \frac{10}{\root \of 2}$$
$$\omega = 5[rad/s]$$
$$\omega が十分大きい時$$
$$20 log_{10}(\frac{10}{\root \of {1 + (0.2 \omega )^2}}) \simeq 20 log_{10}(\frac{10}{0.2 \omega})$$
$$\risingdotseq 34 - 20 log_{10} \omega$$
Ans.(1)
ゲイン余有・位相余有
位相交点：位相曲線が-180°の線を切る点。ゲイン余有：位相交点の周波数におけるゲインの 0 dB との差
ゲイン交点：ゲイン曲線が 0 dBの線を切る点。位相余有：ゲイン交点の周波数における位相の -180 度との差
余有が＋であれば安定、０なら安定限界、−なら不安定
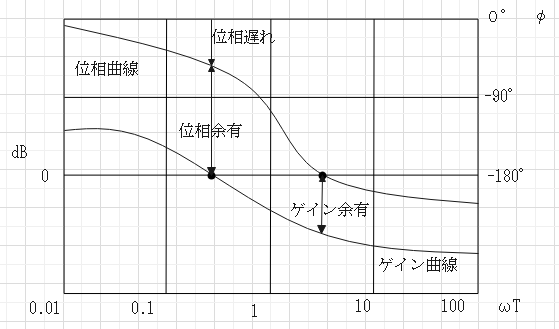
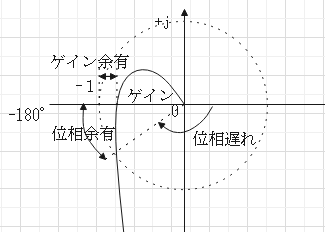
ゲイン余有：位相が-180°となる周波数においてゲインが１に対してどれほど余有があるか。
位相余有：ゲインが１になる周波数においてその位相が-180°に対してどれほど余有があるか
RC・RL回路の伝達関数
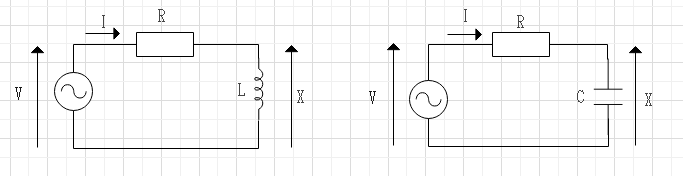$$V(t) = Ri(i) + X(t),X(t) = L \frac{d i(t)}{dt}$$
$$\frac{X(s)}{V(s)} = \frac{X(j \omega)}{V(j \omega)} = \frac{j \omega L}{R + j \omega L}$$
$$V(t) = Ri(i) + X(t),X(t) = \frac 1 c \int{i(t)dt}$$
$$\frac{X(j \omega)}{V(j \omega)} = \frac{1}{j \omega RC +1}$$
(a)
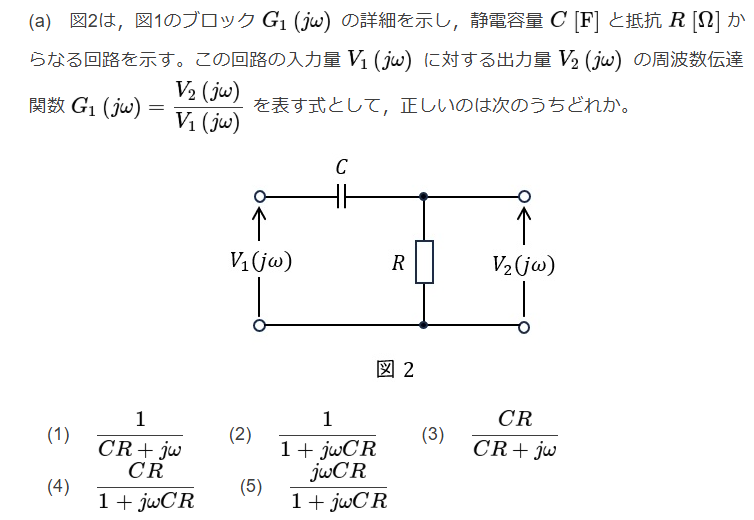
$$V_1(t) = \frac 1 c \int{i(t)dt}+ Ri(i),V_2(t) = Ri(i)$$
$$V_1(j \omega) = \frac{1}{ j \omega c} i(j \omega)+ Ri(j \omega),V_2(j \omega) = Ri(j \omega)$$
$$G_1(j \omega) = \frac{V_2(j \omega)}{V_1(j \omega)} = \frac{1}{j \omega CR +1}$$
Ans.(2)
(b)
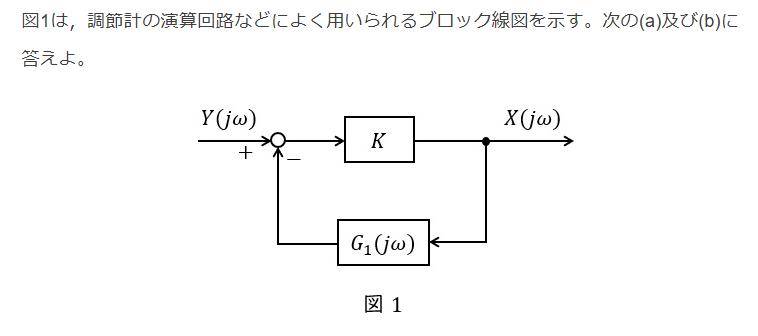
$$G(j \omega) = \frac{K}{1 + K \frac{j \omega CR}{1+ j \omega CR}}$$
$$= \frac{K(1 + j \omega CR)}{1 + j \omega CR + K j \omega CR} = \frac{K(1 + j \omega CR)}{1 + j \omega CR(1 + K)}$$
$$K \gg 0 より $$
$$\fallingdotseq \frac{K(1 + j \omega CR)}{j \omega CR K}$$
$$= 1 + \frac{1}{j \omega CR}$$
Ans.(3)