巻線構造をもった固定子に交流を流すと回転磁界(同期速度)が発生し,その磁界により回転子に誘導起電力が発生し,その起電力による電流と回転磁界の相互作用により回転磁界と同方向に回転力が生じ,回転子が回転する。相互作用によって回転力が発生するためかならず回転磁界の早さよりも回転子の速さが小さい。

 Ans.(2)
Ans.(2)
 Ans.(5)
Ans.(5)
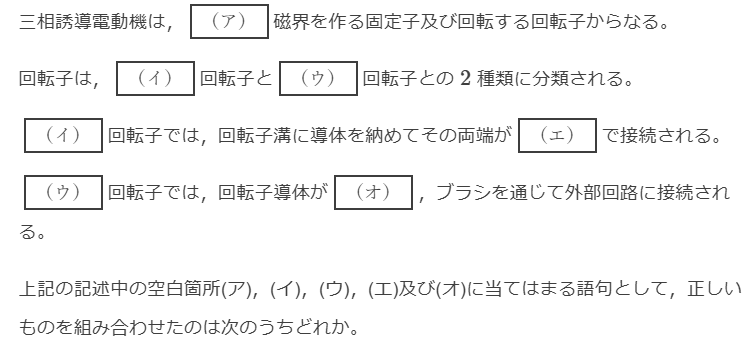 \[
\[\begin{array}{cccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) \\
\hline
(1) & 回 転 & 円筒形 & 巻線形 & スリップリング & 整流子 \\
\hline
(2) & 固 定 & かご形 & 円筒形 & 端絡環 & スリップリング \\
\hline
(3) & 回 転 & 巻線形 & かご形 & スリップリング & 整流子 \\
\hline
(4) & 回 転 & かご形 & 巻線形 & 端絡環 & スリップリング \\
\hline
(5) & 固 定 & 巻線形 & かご形 & スリップリング & 整流子 \\
\hline
\end{array}
\] Ans.(4)
 \[
\[\begin{array}{cccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) \\
\hline
(1) & 回 転 & 円筒形 & 巻線形 & スリップリング & 整流子 \\
\hline
(2) & 固 定 & かご形 & 円筒形 & 端絡環 & スリップリング \\
\hline
(3) & 回 転 & 巻線形 & かご形 & スリップリング & 整流子 \\
\hline
(4) & 回 転 & かご形 & 巻線形 & 端絡環 & スリップリング \\
\hline
(5) & 固 定 & 巻線形 & かご形 & スリップリング & 整流子 \\
\hline
\end{array}
\] Ans.(4)
回転磁界の速度:同期速度$$N_s = \frac{120}{p}f$$ $$f:周波数、p:磁極の数$$
すべり$$s = \frac{N_s - N}{N_s}$$ $$N:回転子の速度(回転速度)$$
$$N = (1 -s)N_s = \frac{120(1-s)}{p}f$$
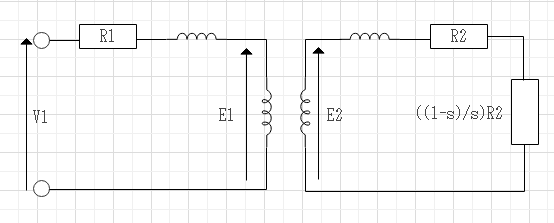
$$固定子入力P_1$$
$$固定子銅損P_{c1} :I_1^2R_1$$
$$回転子入力P_2$$
$$回転子銅損P_{c2}:I_2^2R_2$$
$$機械出力P_o:I_2^2\frac{1-s}{s}R_2$$
$$P_2:P_{c2}:P_o = 1:s:(1-s)$$
トルク$$T = \frac{60P_2}{2 \pi N} = \frac{60P_2}{2 \pi (1-s)N_s}$$
回転子に流れる電流の周波数$$=s ×定格周波数$$

 Ans.(2)
Ans.(2)

$$機械出力=3 \times I_1^2\frac{1-s}{s}R_2$$ $$= 3 \times \frac{1-0.1}{0.1}\times 9 I_1^2 = 243 I_1^2$$ $$一次側銅損= 3 \times 15 \times I_1^2 = 45 I_1^2$$ $$二次側銅損= 3 \times 9 \times I_1^2 = 27 I_1^2$$ $$効率 = \frac{機械出力}{機械出力 +一次側銅損 +二次側銅損}$$ $$= \frac{243}{243 + 45 + 27} = 0.77$$ $$$$ Ans.(2)


(ア)$$s = \frac{N_s - N}{N_s} = \frac{1500-1200}{1500} = 0.2$$ (イ)$$誘導電動機内部の損失はないので1 \times P_{2C}$$ (ウ)$$P_2:P_{c2}:P_m = 1:s:(1-s)$$ $$一次側の損失がないのでP_1 = P_2$$ $$P_{2C} = 0.2 \times P_1$$ (エ)$$P_{2C} = \frac{0.2}{1 - 0.2}\times P_m = 0.25 \times P_m$$ $$$$ Ans.(3)

(a)$$T = \frac{60P_2}{2 \pi N} $$ $$N = \frac{60p_2}{2 \pi T} = \frac{60 \times 7.5 \times 10^3}{2 \pi \times 82} = 873.4$$ $$Ans.(4)$$ (b)$$N_s = \frac{120}{p}f = \frac{120}{8}60 = 900$$ $$s = \frac{N_s - N}{N_s} = \frac{900 - 874}{900} = 0.289$$ $$回転子に流れる電流の周波数$$$$=s ×定格周波数 = 0.289 \times 60 = 1.73 $$ Ans.(1)