電磁気学

静電気

クーロンの法則

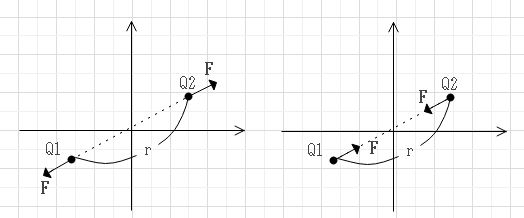
二つの点電荷が距離ｒを隔てておかれている時、両電荷に働く電気力Ｆはその方向が両電荷を結ぶ直線状にあり、その大きさは電荷の量Q₁、Q₂の積に比例し、距離rの２乗に反比例する。Q₁、Q₂が同符号の時Fは反発力、異符号の時は吸引力。

\[ F=\frac{Q_1Q_2}{4\pi\varepsilon_0 r^2} (真空中）\]

$$電荷Q：粒子や物体が帯びている電気の量[C]。真空の誘電率\varepsilon_0[F/m]$$

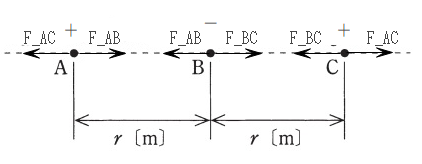
$$三つの点電荷に働く力が釣り合う時はQ_Aが＋なのでQ_Bは−、Q_Cは＋の時のみ。$$ $$Q_AとQ_Bに働く力をF_{AB}、Q_BとQ_Cに働く力をF_{BC}、Q_AとQ_Cに働く力をF_{AC}とすると$$ $$|F_{AC}| = |F_{AB}|,|F_{AB}| = |F_{BC}|$$ $$\frac{Q_A Q_C}{(2r)^2} = \frac{Q_A Q_B}{r^2} = \frac{Q_B Q_C}{r^2}　（4\pi\varepsilon_0は省略）$$ $$３つの電荷の符号があっているのは（２）、（３）、（５）。$$ $$そのうち値を代入して等式が成り立つのがAns（３）$$

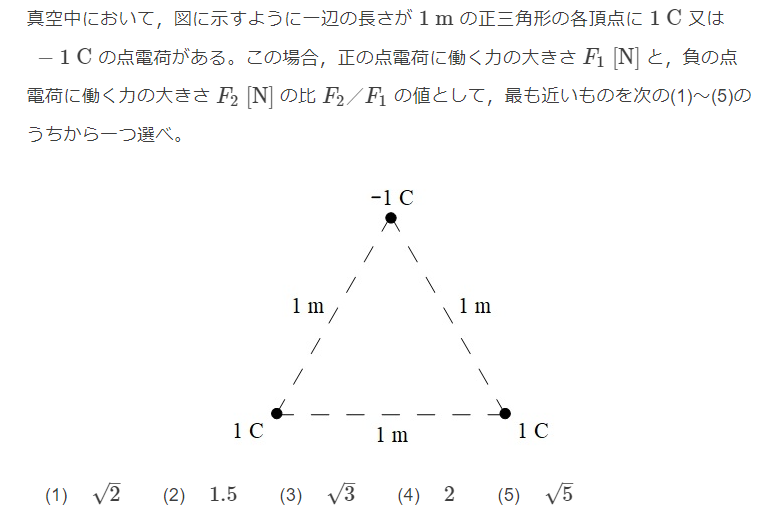
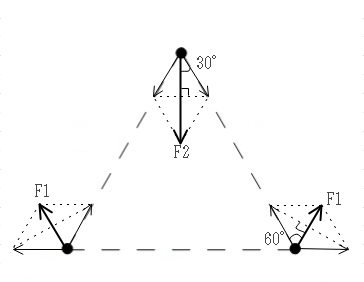
$$F=\frac{1}{4\pi\varepsilon_0 }$$ $$F_1 = 2 \times F \cos{60°} = F$$ $$F_2 = 2 \times F \cos{30°} = \sqrt3 F$$ $$\frac{F_2}{F_1} = \sqrt3 。Ans（３）$$ $$$$ $$$$

電界

電界とは電荷による 静電気力（クーロン力）が働く空間。電場。

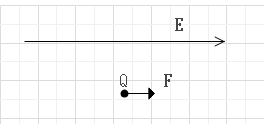
電界内の１点に点電荷を置いたとき、その１[C]あたりに働く電気力（静電力）をその点の電界の強さという。電界の強さＥの電場に点電荷Ｑをおくと点電荷に力Ｆが働く。

Ｆ＝ＱＥ

Ｅ：電界の強さ（電界）[N/C]、[V/m]

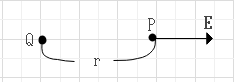
点電荷Qが点Ｐに生じる電界の大きさＥは点Ｐ＝1[C]の時に点Ｐに働く力の大きさなので、$$E=\frac{F}{1}$$

$$E=\frac{Q}{4\pi\varepsilon_0 r^2}$$

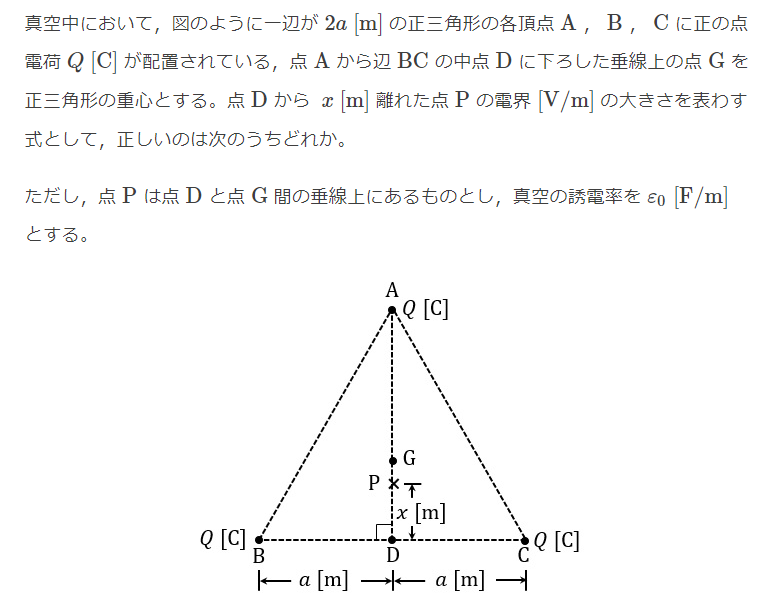
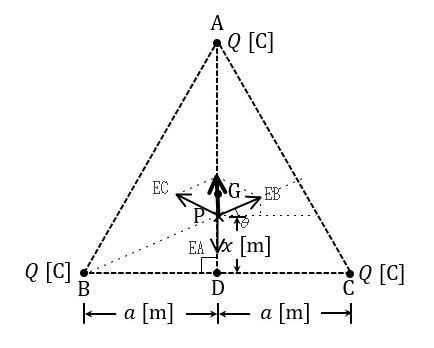
$$∠AQD = 60°より\bar{AP} = \sqrt3a - x ,\bar{BP} = \bar{CP} = \sqrt{a^2 + x^2}$$ $$点Aによる電界の強さE_A = \frac{Q}{4\pi\varepsilon_0 (\sqrt3a - x)^2}$$ $$点Bによる電界の強さE_B = \frac{Q}{4\pi\varepsilon_0 (a^2 + x^2)}$$ $$点Cによる電界の強さE_C = E_B$$ $$E_BとE_Cの合成電界E_{BC} = 2E_B sin(θ)。sin(θ) = \frac{x}{\sqrt{a^2 + x^2}}$$ $$下向きの力を正とすると点Pの合成電界E_P = E_A - E_{BC}$$ $$= \frac{Q}{4\pi\varepsilon_0 (\sqrt3a - x)^2} - 2\frac{Q}{4\pi\varepsilon_0 (a^2 + x^2)}\frac{x}{\sqrt{a^2 + x^2}}$$ $$= \frac{Q}{4\pi\varepsilon_0}{\frac{1}{(\sqrt3a - x)^2}} - \frac{2x}{(a^2 + x^2)^{\frac{3}{2}}}$$ $$Ans（５）$$

電位・電位差（電圧）

電位とは電界に逆らって無限遠点からある地点まで単位点電荷１[C]を運ぶとき外部からなす仕事。[V]、[J/C]。電位の傾きは電界の強さ。

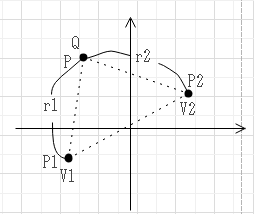
$$V_1=\frac{Q}{4\pi\varepsilon_0 r_1},V_2=\frac{Q}{4\pi\varepsilon_0 r_2},V=V_2-V_1$$

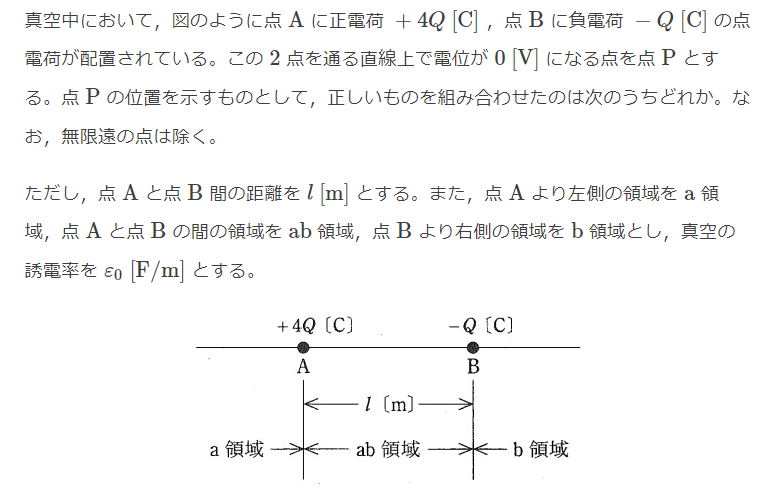
$$a領域：点Aからの距離をｘとすると$$ $$V = \frac{Q}{4\pi\varepsilon_0}(\frac{4}{x} - \frac{1}{l+x})$$ $$\frac{4}{x} - \frac{1}{l+x} = 0なので、x = -\frac{4}{3}<0 なので存在しない$$ $$ab領域：点Aからの距離をｘとすると$$ $$V = \frac{Q}{4\pi\varepsilon_0}(\frac{4}{x} - \frac{1}{l-x}),x = \frac{4}{5}l$$ $$b領域：点Bからの距離をｘとすると$$ $$V = \frac{Q}{4\pi\varepsilon_0}(\frac{4}{l + x} - \frac{1}{x}),x = \frac{1}{3}$$ $$Ans（２）$$

電気力線

電気力の様子を視覚的に表現するための仮想的な線。

正の電荷から負の電荷へと向かう線。電気力線の向きは電界の向きと一緒。電荷のないところで途切れたり二つ以上の線が交わったりすることはない。電気力線の本数はその場所の電気量に比例する。

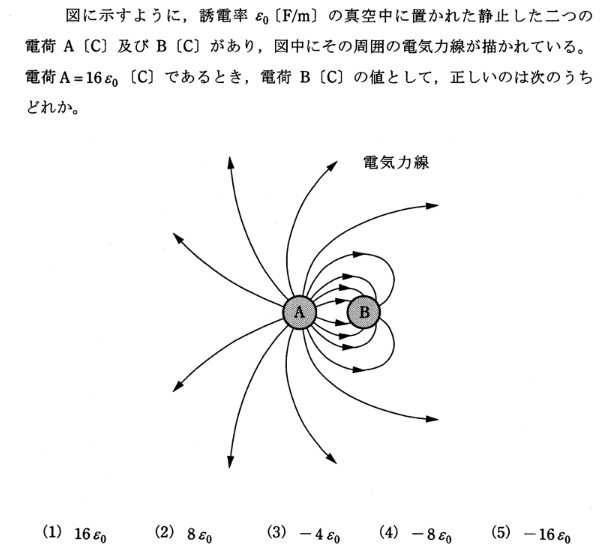
電気力線の本数はその場所の電気量に比例する。電荷Aからは電子力線が１６本で１６ε₀、電荷Bからは８本なので８ε₀。電気力線は電荷AからBに向かっているので電荷Bは-。よってAns（４）

$$（１）F=\frac{Q_1Q_2}{4\pi\varepsilon_0 r^2}　電気量の積に比例するので×$$ $$（２）E=\frac{Q}{4\pi\varepsilon_0 r^2}　距離の二乗に反比例するので×$$ $$（３）電気力線の向きは電界の向きと一緒なので○$$ $$（４）等電位面に垂直な方向に働くので×$$ $$（５）Ｅ＝\frac{σ}{ε}　比例して減少するので×$$ $$$$

静磁気

クーロンの法則

二つの磁極が距離ｒを隔てておかれている時、両磁極に働く磁気力Ｆはその方向が両磁極を結ぶ直線状にあり、その大きさは磁極の大きさｍ₁、ｍ₂の積に比例し、距離ｒの２乗に反比例する。ｍ₁、ｍ₂が同符号の時Ｆは反発力、異符号の時は吸引力。

$$F=\frac{m_1m_2}{4\pi \mu_0 r^2} （真空中）$$

磁極の強さｍ：磁極が帯びている磁気の量[Wb]。真空の透磁率μ₀[H/m]

磁界

磁界とは磁極による 静磁力が働く空間。磁場。

磁界内の１点に磁極を置いたとき、その１[Wb]あたりに働く静磁力をその点の磁界の強さという。

磁極ｍがある点に生じる磁界の大きさＨはある点1[Wb]の時に働く力の大きさ。

$$H=\frac{m}{4\pi \mu_0 r^2} [A/m]$$

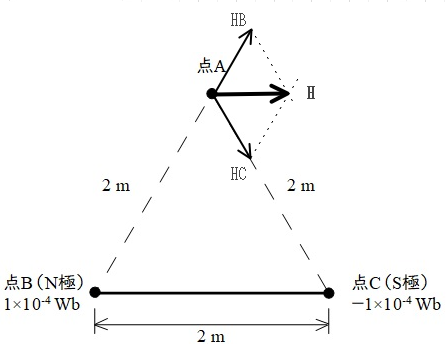
$$H = H_B cos(60°) + H_C cos(60°) = H_B = H_C$$ $$H=\frac{m}{4\pi \mu_0 r^2} $$ $$= \frac{1 \times 10^{-4}}{4\pi \times 4\pi \times 10^{-7} 2^2} ≒1.58$$ $$Ans（４）$$ $$$$ $$$$

磁力線

磁気力の様子を視覚的に表現するための仮想的な線。

正の磁極から負の磁極へと向かう線。磁力線の向きは磁界の向きと一緒。磁極のないところで途切れたり二つ以上の線が交わったりすることはない。磁力線の本数はその場所の磁界の強さに比例する。

磁束密度

磁界の強さを表す量。 磁界の中で、磁界に垂直な断面の単位面積当たりに通っている磁束。

$$\bf{B}＝\mu_0\bf{H} [T]、[Wb/m^2]$$

磁束

その場における磁界の強さと方向を、1(Wb)を1本とした線の束で表したもの

$$\phi=BS[Wb]$$

Ｓ：磁束線に垂直な平面の面積

電流磁界

フレミングの左手の法則

左手の中指、人差し指、親指を互いに直角にしたとき、中指の方向が電流Ｉ、人差し指の方向が磁界密度Ｂの方向とすると、電磁力Ｆは親指の方向に向かう。

$$導線にかかる力F =B I l sinθ　。l:導線の長さ[ｍ]、θ = ∠（I,B）電流の向きと磁界の向きとのなす角度$$

Ans.（５）

アンペアの右ねじの法則

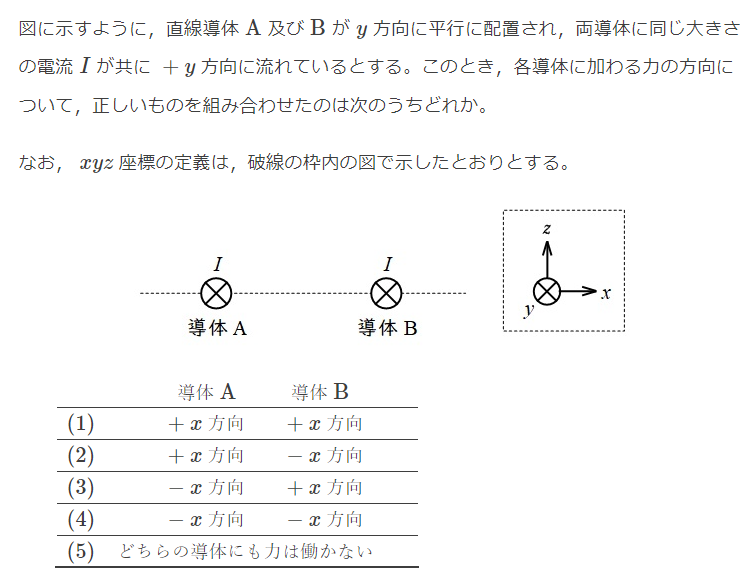
右ねじをＨの方向に回す（時計回り）とき、そのねじの進む方向がＩの進む方向になる。

アンペアの右ねじの法則により導体Aの電流による磁界の向きは導体Bの位置では-ｚ方向。同様に導体Bの電流による磁界の向きは導体Aの位置でｚ方向。 フレミングの左手の法則により、導体Aが受ける電磁力の向きはx方向、導体Bが受ける電磁力の向きは-x方向。よってAns.（2）

アンペアの周回積分の法則

単位磁極をある点から出発させて閉局面Cに沿って動かし元の点に戻すときに磁界Ｈがする仕事が電流Ｉと等しい。磁界を周回積分したものは、その中に流れる電流と等しい。

無限長直線電流

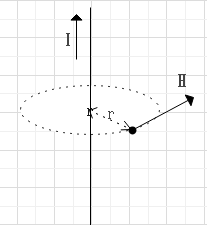
$$H=\frac{I}{2\pi r}$$

$$一方の導体が受ける力F =B \times 10 \times 1 = 1 \times 10^{-6}$$ $$一方の導体の磁束密度　B = \mu_0 H = \frac{4\pi \times 10^{-7} \times I}{2 \pi \times 0.2}$$ $$I = \frac{1 \times 10^{-6} \times 2 \pi \times 0.1}{10 \times 4\pi \times 10^{-7}} = 0.1$$ $$Ans. (1) $$ $$$$ $$$$

円形電流

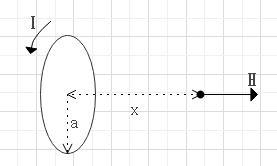
$$H=\frac{Ia^2}{2(a^2+x^2)^\frac{3}{2}}$$

コイル

ビオ・サバールの法則

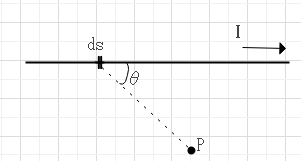
電流要素Ｉdsが空間内の任意の点Ｐにある強さｍの磁極に及ぼす力dFとすると、Ｐ点の磁界dＨ＝dF／ｍがＩ ds sinθに比例し、dsとＰ間の距離ｒの二乗に反比例する。

$$dH=\frac{I ds sin\theta}{4\pi r^2}$$ 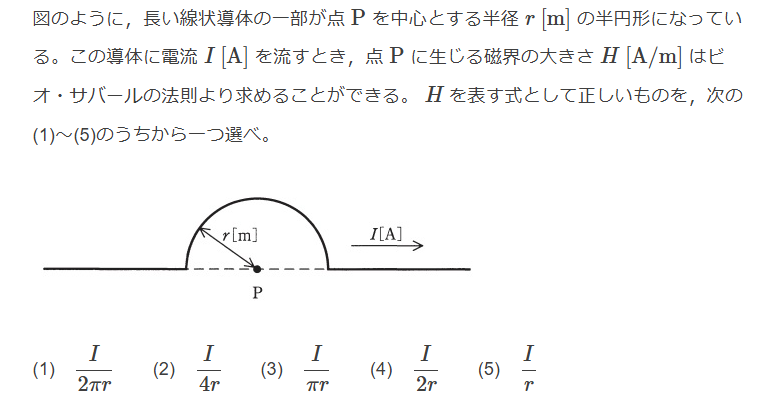$$半円形の長さ（dsの総和）= \pi r ,\sin{180°}=0より$$ $$H = \frac{I \times \pi r}{4 \pi r^2} = \frac{I}{4r}$$ $$Ans.(2)$$ $$$$

電磁誘導

レンツの法則

回路を通り抜ける磁束が変化するときには、その変化を妨げるような方向に電流を流そうとする起電力が誘導される。

$$誘導起電力e=-\frac{d\Phi}{dt}$$

$$磁束数\Phi＝N\phi[Wb]。N：コイルの巻き数。\phi：磁束$$

フレミングの右手の法則

右手の中指、人差し指、親指を互いに直角の方向に向けた時、親指の方向を導体の運動の方向、人差し指を磁束密度とすると、誘導電界にしたがって起電力は中指の方向に向かう。

導線が一様磁界中で平行移動する場合

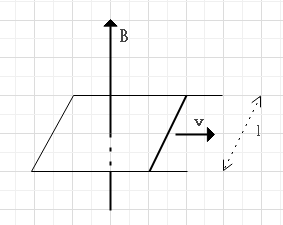
コの字に曲げた導線の上を、一定速度ｖ[m/s]で長さｌ[m]の導線を移動、移動する導線はコの字の導線の一辺と並行、導線に垂直な一様磁束密度Ｂ[T]。

$$e= v B l[V]$$

長方形コイルが一様磁界中で回転する場合

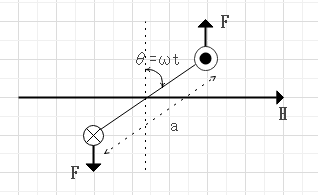
一様磁界Ｈ[A/m]中に２辺の長さがa[m]、b[m]、巻き数Ｎの長方形コイルをその鉛直なa辺の中点を通りＨに垂直な水平軸周りに角速度ω[rad/s]で回転させる場合。

$$磁束数\Phi=\mu_0 H N a b \cos{\omega t} [Wb]$$

$$e=-\frac{d\Phi}{dt}=\omega\mu_0 H N a b \sin{\omega t}$$

自己インダクタンスＬ[H]

電流とそれによって作られる磁界の強さは比例するので透磁率が一様の場合磁束数は電流に比例する。その比例定数をＬとする。コイルの巻き数Nの場合。

$$N \Phi=LI$$

相互インダクタンスＭ[H]

二つの回路が対立して一方の電流が変化すると、磁束が変化して、他方に起電力が発生する。この現象を相互誘導という。その比例定数をMとする $$自己インダクタンスL_1とL_2のコイルがあった場合の相互インダクタンスは M = k \sqrt{L_1 L_2} 0 \leqq k \leqq 1 (k:結合係数)$$

無端ソロノイドの自己・相互インダクタンス

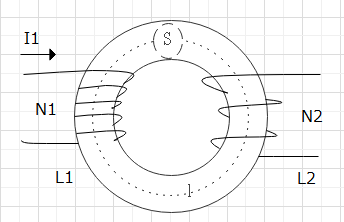
断面積Ｓ，平均磁路長l、透磁率μの環状鉄心にそれぞれ巻き数N1、N2のコイルを巻いている。

$$起磁力\mathscr{F}=NI ｢A｣、磁気抵抗\mathscr{R}=\frac{l}{\mu S}[H^{-1}]、\phi=\frac{\mathscr{F}}{\mathscr{R}}=\frac{\mu NIS}{l}$$

$$N1のコイルに電流Ｉ_1を流したときに生じる磁束数\Phi_1=N1\phi_1=\frac{\mu N1^2I_1 S}{l}、 \Phi_2＝N2\phi_1=\frac{\mu N1N2I_1S}{l}、$$ $$L1=\frac{\Phi_1}{I_1}=\frac{\mu N1^2S}{l}、L2=\frac{N2 \phi_2}{I_2}=\frac{\mu N2^2S}{l}、$$ $$M=\frac{\Phi_2}{I_1}=\frac{\mu N1N2S}{l}$$

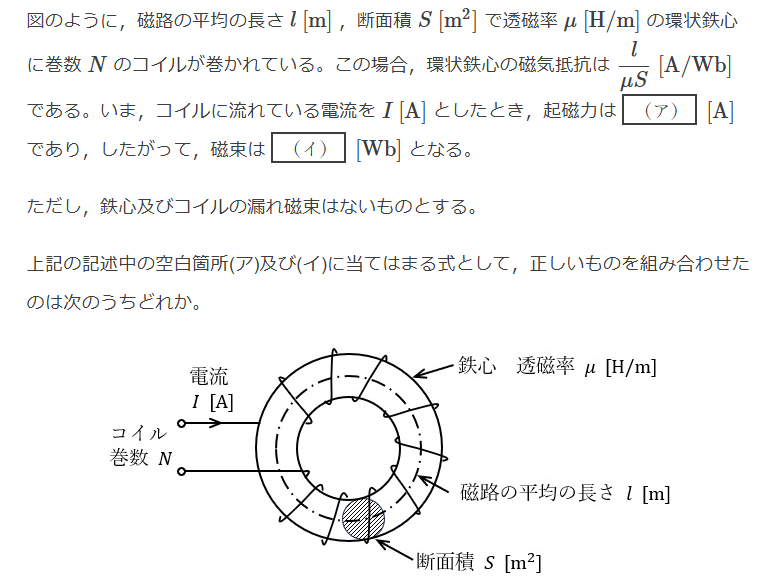
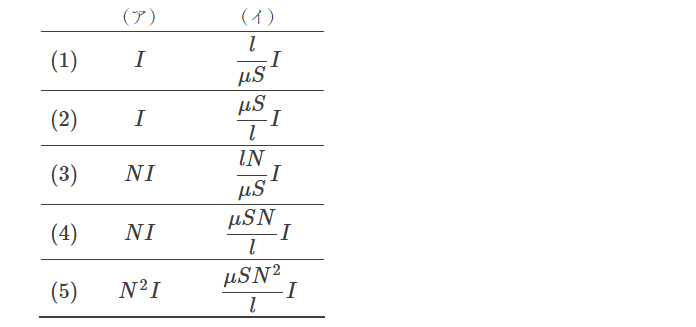
$$（ア）\mathscr{F}=NI$$ $$（イ）\phi=\frac{\mathscr{F}}{\mathscr{R}}=\frac{\mu NIS}{l}$$ $$Ans.（４）$$ $$コイル１の自己インダクタンスL=\frac{\mu N^2S}{l}$$ $$コイル２の自己インダクタンス4L = \frac{\mu n^2S}{l}$$ $$4 \times \frac{\mu N^2S}{l} = \frac{\mu n^2S}{l}$$ $$n = 2 N$$

$$L=\frac{\mu N^2S}{l}　$$ $$（ア）２乗（イ）長さ$$ $$（ウ）多く$$ $$（エ）k=1の時　\sqrt{L_1 L_2}$$ 二つのコイルを接続したときの合成インダクタンス $$和動接続（二つのコイルに生じる磁束の向きが一緒）L = L_1 + L_2 + 2M$$ $$差動接続（二つのコイルに生じる磁束の向きが逆）L = L_1 + L_2 - 2M$$ $$（オ）和動接続　　Ans.(5)$$

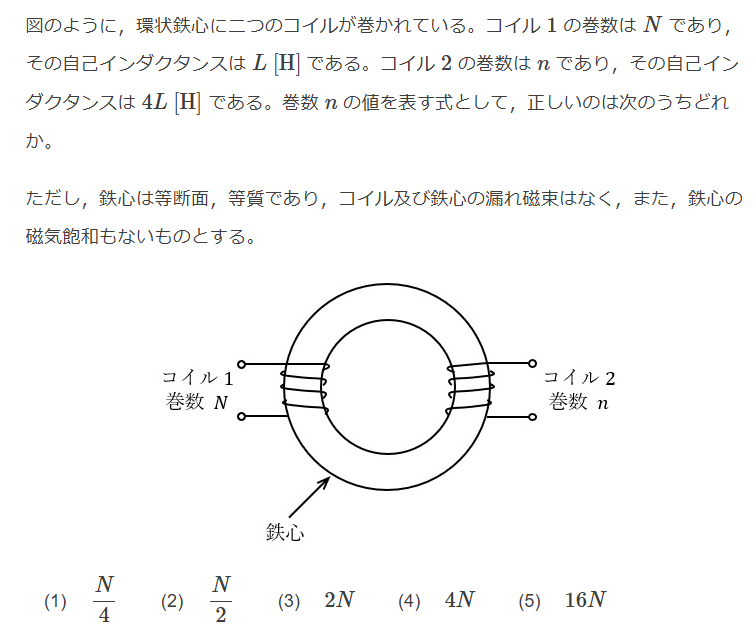
$$M = k\sqrt{L_1 L_2} = k\sqrt{40 \times 10} = 20k[mH]$$ $$二つのコイルは和動接続なので$$ $$L = L_1 + L_2 + 2M$$ $$86 = 40 + 10 +2 \times 20k$$ $$k = 0.9 Ans.(2)$$ $$$$

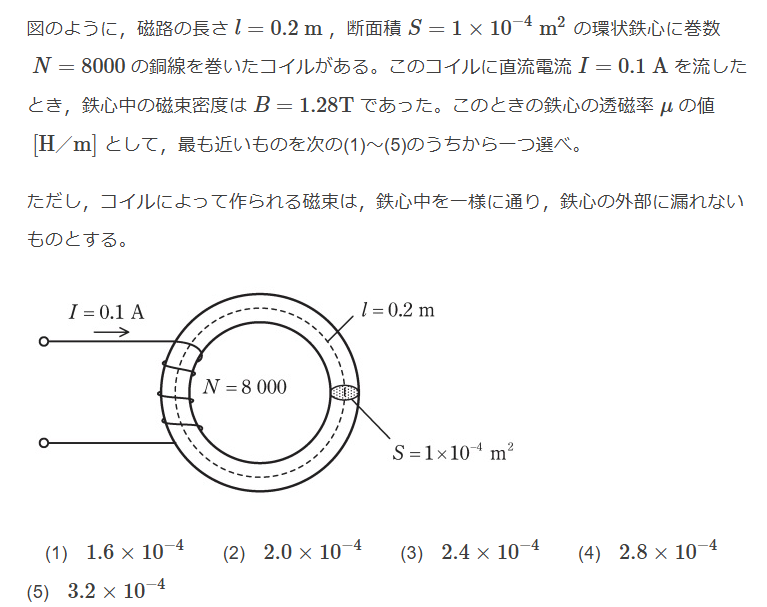
$$H l = N I , B = \mu H より$$ $$または\phi=\frac{\mu NIS}{l},\phi = BS より$$ $$B = \frac{\mu NI }{l}$$ $$\mu = \frac{B l}{NI}$$ $$ = \frac{1.28 \times 0.2}{8000 \times 0.1}$$ $$= 3.2 \times 10^{-4}[H/m] Ans.(5)$$

ヒステリシス曲線

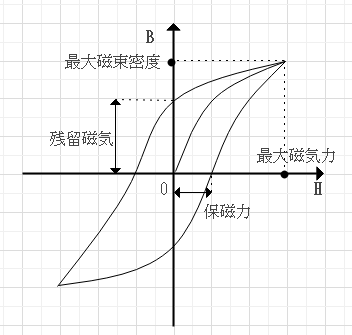
B：磁束密度とH：磁界の強さの関係を表す曲線。磁性体に磁界を加えると磁化する。

０点は磁性体が磁化していない状態。磁界を加えると磁性体が磁化して磁束密度が増加する。際限なく増加するわけではなく最大（飽和）磁束密度までしか増えない。

付加する磁界を減らしていくと磁束密度も減っていく。磁界を０にしても磁束密度は０にはならず、磁性体は磁化したままでその時の磁束密度を残留磁気（磁束密度）という。

逆向きの磁界を付加していくとある点で磁束密度が０になる。その時の磁界の強さを保磁力という。

残留磁気が大きく保磁力が小さい磁性体は電磁石に適し、残留磁気と保磁力が大きい磁性体は永久磁石に適している。

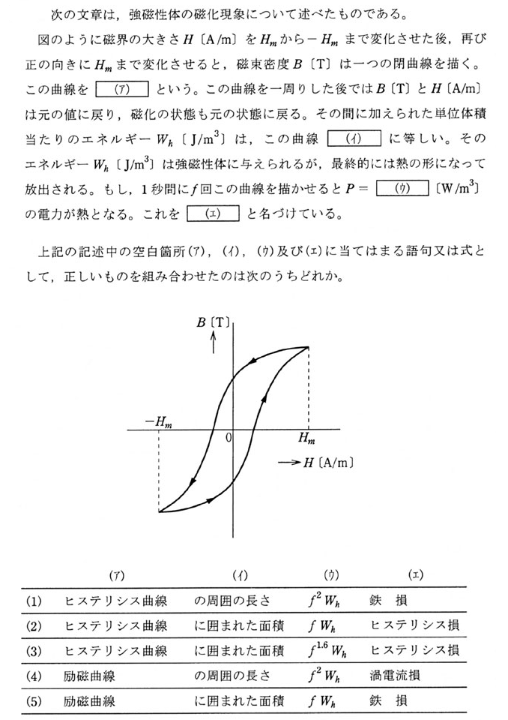
$$（ア）ヒステリシス曲線$$ $$（イ）囲まれた面積$$ $$（ウ）fW_h$$ $$（エ）ヒステリシス損$$ $$Ans.（２）$$ $$$$

$$（ア）電流が最大の時はHも最大。$$２$$ $$（イ）周波数が低下するとコイルのリアクタンスが増加、電流が増加$$大きくなる$$ $$（ウ）電圧が低下すると電流も低下$$小さくなる$$ $$（エ）電流の実効値が一定$$あまり変わらない$$ $$Ans.(2)$$