�d�C��H[����]/ �d���C�w/ �d�C��H[��]/ �d�C��H[�O����]/ �d�q��H
�Ȋw�̕���[�H�w�E���w]
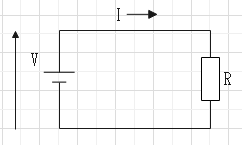
�I�[���̖@���Ƃ͓d�C��H�œ�_�Ԃ̓d���͂����ɗ����d���ɔ�Ⴗ��B�d���͓d���ƒ�R�̐ςŕ\�����B
$$�u���q�h�B�d��[V]����R[��]�~�d��[A]$$
$$�d��[W]�F�o���u�h���q�h^2$$
�����̒�R����ł������ꍇ�̒�R�l�̌v�Z���@�B�����̏ꍇ����ڑ��ƕ���ڑ��̕����^�Ȃ̂ŁA���ꂼ��̌v�Z���@���킩���Ă���Α����̓d�C��H�̍�����R���v�Z�ł���B
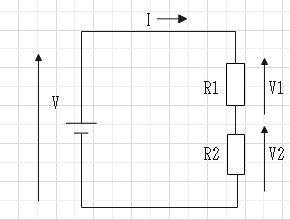
��R������ɐڑ�����Ă���ꍇ�́A�e��R�l�̘a�ō�����R������킳���B
�d���͂ǂ̒�R���������̂������B�d���͒�R�ɉ����ĕ��z�����B
$$�q���q_1�{�q_2�B�u���u_1�{�u_2�B�h��\frac{�u}{�q}$$
$$�u_1��\frac{�q_1}{�q_1�{�q_2}�u�A�u_2��\frac{�q_1}{�q_1�{�q_2}�u$$
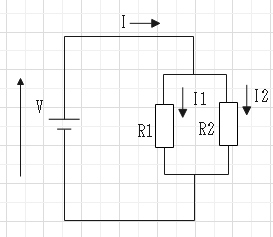
��R������ɐڑ�����Ă���ꍇ�́A������R�̋t�����e��R�l�̋t���̘a�ŕ\�����B
�d���͒�R�l�ɉ����ĕ��z�����B�d���͂ǂ̒�R�ɂ��������̂�������B
$$\frac{�P}{�q}��\frac{�P}{�q_1}�{\frac{�P}{�q_2}�A�q��\frac{�q_1�q_2}{�q_1�{�q_2}$$
$$�h���h_1�{�h_2�A�h_1��\frac{�q_2}{�q_1�{�q_2}�h�A�h_2��\frac{�q_1}{�q_1�{�q_2}�h$$

$$����ڑ��̍�����R�@R_1 + R_2 = \frac{30[V]}{6[A]} = 5[\Omega]$$ $$����ڑ��̍�����R�@\frac{R_1R_2}{R_1�{R_2} = \frac{30[V]}{25[A]} = 1.2[\Omega]$$ $$R_2 = 5 - R_1 �����ڑ��̍�����R�̎��ɑ�� $$ $$\frac{R_1(5 - R_1)}{R_1�{5 - R_1} = 1.2, R_1^2 -5R_1 + 6 =0$$ $$R_1 = 2,3 ,R_2 = 3,2 �����Ans�i�S�j$$

�P�D�}�̒�����H�ɂ�����R=20[��]�̏ꍇ�̉�H�̍�����R�����߂�B
$$30 + \frac{12 \times 20}{12 + 20}=37.5[\Omega]$$
�Q�D12[��]�̒�R�̏���d�͂����߂�B
$$��R30[\Omega]�ɗ����d��I_{30} = \frac{90}{37.5} = 2.4[A]$$ $$��R12[\Omega]�ɗ����d��I_{12} = \frac{20}{12 + 20} \times I_{30} = 1.5[A]$$ $$����d�͂́A12 \times {1.5}^2 = 27[W]$$ $$$$
�d�C��H�ɂ�����d���Ɠd���̑��a�̖@���B
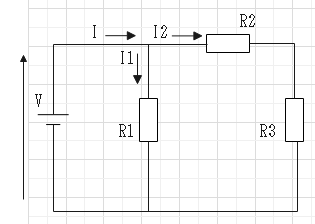
���@���F�C�ӂ̐ߓ_�ɗ�������}�d���̘a�͂O�B����_�ɑ��ē����Ă���d���̑��a�Əo�Ă����d���̑��a�͓������B
$$�h�|�h_1�|�h_2���O$$
���@���F�C�ӂ̕H�ɂ����āA�H�̉������}�d���̘a�͂O�B��M�����ł���d�C��H�̈ꕔ���ł͓d���̑��a���O�ɂȂ�B
$$�u���q_1 �h_1�A�O���i�q_2�{�q_3�j�h_2�|�q_1�h_1�A�u���i�q_2�{�q_3�j�h_2$$

$$\begin{eqnarray} \left\{ \begin{array}{l} I_1 = I_2 + I_3\\ 4I_1 + 5I_3 -4 =0\\ 2I_2-5I_3 -2 = 0\nonumber \end{array} \right. \end{eqnarray}$$ $$�A���������������ƁAI_1 = 1, I_2 = 1, I_3 = 0�B Ans�i�R�j$$


$$�H�Ɋҗ�����d��I_1,I_2,I_3��}�̂悤�ɒ�`�BI_2�����߂�$$ $$\begin{eqnarray} \left\{ \begin{array}{l} 60 = 40I_1 + 40(I_1 - I_2)\\ 0 = 10I_2 + 60(I_2 + I_3) + 40(I_2 -I_1)\\ 80 = 60I_3 + 60(I_3 + I_2)\nonumber \end{array} \right. \end{eqnarray}$$ $$����ό`����\begin{eqnarray} \left\{ \begin{array}{l} 60 = 80I_1 -40I_2\\ 0 = 110I_2 + 60I_3 - 40I_1\\ 80 = 120I_3 + 60I_2\nonumber \end{array} \right. \end{eqnarray}$$ $$�A����������������I_2 = -\frac16$$ -���t���Ă�̂Őݒ�̓d���̌������t $$����d�͂́@10 \times (\frac{1}{6})^2 = 0.28[W] . Ans(�P)$$ $$$$ $$$$ $$$$

$$�u���b�W��H�̕��t�����FIa = 0�̎�$$
$$R_1R_4 = R_2R_3$$

$$���t��ԂȂ̂ŁA2R_4 = 8R_3��R_4 = 4R_3$$ $$������R�́A\frac{E[V]}{\frac{E}{4}[A]} = 4$$ $$= \frac{2 \times 8}{2 +8} + \frac{4R_3^2}{R_3 + 4R_3}$$ $$R_3^2 = 3R_3 R_3 \ne 0 �Ȃ̂ŁA$$ $$R_3 = 3�BAns�i�R�j$$ $$$$

�X�C�b�`���J���Ă��d�����ς��Ȃ��̂ŁA���t��ԁB�X�C�b�`�ɗ����d���͂O $$������R��\frac{100[V]}{30[A]} = \frac{10}{3}[\Omega]$$ $$�X�C�b�`�����Ă��鎞�AR_3,R_4�̍�����R�́A\frac{10}{3} - \frac{8 \times 4}{8+4}$$ $$\begin{equation}= \frac{2}{3} = \frac{R_3 \times R_4}{R_3 + R_4} \tag{�@} \end{equation}$$ $$���t�������@\begin{equation}8 R_4 = 4 R_3 �� 2R_4 = R_3 \tag{�A} \end{equation}$$ $$�@�A�A���AR_4 = 1[\Omega]�BAns�i�Q�j$$ $$�@�̑���ɁA�X�C�b�`���J���Ă���ꍇ�̓d��$$ $$30[A] = \frac{100}{8 + R_3} + \frac{100}{4 + R_4}��p���Ă��悢 $$
��H���ɓd����E1,�c,Em�A�d����J1,�c,Jn������Ƃ��A��H���̔C�ӂ̓d���E�d���͎��́im+n�j���̏ꍇ�ɑ�������������킹��Γ�����B
�iE1=E1,E2=0,�c,Jn=0�j,�iE1=0,E2=E2,�c,Jn=0�j,�c,�iE1=0,E2=0,�c,Jn=Jn�jE=0�F�Z���AJ=0�F�J��

$$�X�C�b�`���J���Ă���ꍇ�@I_R = I = 2[A]$$ $$�X�C�b�`�����Ă���ꍇ�@I_R = 2I = 4[A]$$ $$�X�C�b�`�����Ă���ꍇ��I_R�́A��d����E��Z�������ꍇ�̓d��I_{RI}��$$ $$��d����I���J�������ꍇ�̓d��I_{RE}�Ƃ̘a�ɂȂ�B$$ $$I_{RI} = \frac{r}{r+R}I = \frac{2}{1+R}$$ $$I_{RE} = \frac{E}{r+R} = \frac{10}{1+R}$$ $$I_R = I_{RI} + I_{RE} = \frac{2}{1+R} + \frac{10}{1+R} = 4 ���@R = 2$$

�Q[V]�̓d����Z��������H�ƂS[V]�̓d����Z��������H�ɕ�����B���ꂼ��̉�H�ŋ��߂�I1,I2,I3�𑫂����킹��ƌ��̉�H�̓d���ɂȂ�BI3�̌����ɒ��ӂ���B

$$������R��4 + \frac{2 \times 5}{2+5} = \frac{38}{7}$$ $$I_1 = 4 \div \frac{38}{7} = \frac{14}{19}$$ $$I_2 = \frac{14}{19} \times \frac{5}{7} = \frac{10}{19}, I_3 = \frac{14}{19} \times \frac{2}{7} = \frac{4}{19}$$ $$$$ $$$$ $$$$ $$$$

$$������R��2 + \frac{4 \times 5}{4+5} = \frac{38}{9}$$ $$I_2 = 2 \div \frac{38}{9} = \frac{9}{19}$$ $$I_1 = \frac{9}{19} \times \frac{5}{9} = \frac{5}{19}, I_3 = \frac{9}{19} \times \frac{4}{9} = \frac{4}{19}$$ $$��̉�H�̓d���𑫂����킹��ƁAI_1 = \frac{14}{19}+\frac{14}{19} =1,$$$$ I_2 = \frac{10}{19} + \frac{9}{19} = 1, I_3 = \frac{4}{19}-\frac{4}{19} =0�B Ans�i�R�j$$

N0��N�͓Ɨ�������H�ŁAN0�ɂ͓����d��������N�ɂ͂Ȃ��B$$N0��N���Ȃ�N0����N�ɗ����d���h��\frac{�u_0}{�y_0�{�y}$$
$$�u_0��N0�̊J���d���A�y��N�̃C���s�[�_���X�A�y_0��N0�̓����d�����Ȃ�������Ԃł̃C���s�[�_���X�B$$�i�C���s�[�_���X�͓d���Ɠd���̔�B������H���ƒ�R�j
$$�d�������߂��������ʼn�H����iN0��N�ɑ����j$$
$$�u_0�����߂�B$$
$$�y_0�����߂�B�iN0���̓����d�����Ȃ����č�����R�����߂�[�d�����͒Z���A�d�����͊J��]�j$$
$$�y�����߂�B�iN�̍�����R�����߂�j$$
$$�d���h��\frac{�u_0}{�y_0�{�y}���v�Z����B$$

$$�d�������߂�������(��RR)�ʼn�H����$$

$$V_0 = \frac{60}{2} - \frac{40}{2} = 10$$ $$Z_0 = \frac{40 \times 40}{40 + 40} + \frac{60 \times 60}{60 + 60} = 20 + 30 =50$$ $$Z = R =10$$ $$I = \frac{V_0}{Z_0�{Z} = \frac{10}{50 + 10} = \frac16$$ $$����d�͂�RI^2 = 10 \times \frac{1}{6}^2 = 0.28[W] . Ans(�P)$$ $$$$ $$$$

$$�d�������߂�������(��RR)�ʼn�H����$$
$$V_0 = E = 9V$$ $$Z_0 = \frac{0.1}{4} = 0.025\Omega$$ $$Z = R = 0.5\Omega$$ $$I = \frac{V_0}{Z_0�{Z} = \frac{9}{0.025 + 0.5} = 17.143$$ $$����d�͂�RI^2 = 0.5 \times 17.143^2 = 146.9[W] . Ans(�Q)$$ $$$$ $$$$
$$�u��\frac{�h_0}{�x_0�{�x}$$
�u�FN�̒[�q�Ԃɂ�����d���B�h0�FN0�P�Ƃ̒Z���d���i�[�q�Ԃ�Z���j�B�x0�FN0�����d�����O������̍����A�h�~�^���X�B�x�FN�̍����A�h�~�^���X�i�A�h�~�^���X�͓d���Ɠd���̔�B������H���ƒ�R�̋t���j
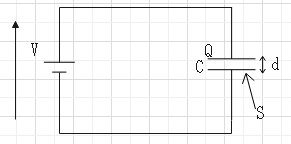
$$�p���b�u�A�b��\frac{�p}{�u}.�Ód�e��[F]��\frac{�d��[C]}{�d��[V]}$$
$$�p���Ђr.�b��\frac{�Ђr}{�u}��\frac{�Âr}{d}.(�d��\frac{��}{��}.�u���d d ��\frac{��d}{��})$$�ЁF�\�ʓd�ז��x[C/m2]�A�r�F�R���f���T�̋ɔʐ�[m2]�Ad�F�ɔŊԋ���[m]�A�ÁF��U�d��[F/m]�A�d:�R���f���T���̓d�E�̋���[V/m]
$$�Ód�G�l���M�[W = \frac12QV = \frac12CV^2 [J]$$

$$(1) �p���b�u ���p���b\frac{��d}{��}���b��\frac{�p��}{��}\frac1d�@����ā�$$
$$(2)�p���b�u ���p���b�d d��\frac{�Âr}{d}�d d�@= �Âr�d ���d ��\frac{�p}{�Âr}����ā~$$
$$(3)�p���b�u ���p��\frac{�Âr}{d}�u ���u��\frac{�p}{�Âr}d����ā�$$
$$(4)�u���d d �@�� �d��\frac{�u}{d}����ā�$$
$$(5)�p��\frac{�Âr}{d}�u����ā�$$

$$W = \frac12CV^2 = \frac12(\frac{�Âr}{d})(\frac{E}{d})^2 = \frac12 �� E^ (Sd) = \frac12 �� E^ V $$ $$�����Ans�i�S�j$$ $$$$ $$$$ $$$$ $$$$ $$$$
$$��U�d��\varepsilon_S�F�^�̗U�d��\varepsilon_0�Ƃ̔� \varepsilon = \varepsilon_S \varepsilon_0$$ $$���̒��̓d�E�A�d�ʍ��O�i�d�ׂ����̂̕\�ʂɏW�܂邽�߁j$$ $$�d�����xD = \frac{�p}{�r}=\varepsilon E [C/m^2]$$

$$�i�A�j�u���d d ���AE_1 = \frac{V_0}{d},E_2 = \frac{V_0}{d}$$ $$�i�C�jD = \varepsilon E���AD_1 = {\varepsilon_0\varepsilon_1}{d}V_0,D_2 = {\varepsilon_0\varepsilon_2}{d}V_0$$ $$�i�E�j�p���b�u,\frac{\varepsilon�r}{d}�iD = \frac{�p}{�r}�j���AQ_1 = {\varepsilon_0\varepsilon_1}{d}SV_0,Q_2 = {\varepsilon_0\varepsilon_2}{d}SV_0$$ $$$$ $$$$ $$$$ $$$$

$$�ɔ�A-P�Ԃ�Q-B�Ԃ�ʁX�̃R���f���T�ƍl����B���҂̓d��Q�͈ꏏ�B�ɔ̖ʐς�S�Ƃ���B$$ $$C_{AP} = \frac{\varepsilon_r\varepsilon_0}{\frac12}, C_{QB} = \frac{\varepsilon_r\varepsilon_0}{\frac14}��C_{AP} = 2C_{QB}$$ $$�p���b�u���2V_{AP} = V_{QB},V_{AP} =\frac{2}{3}V_0,V_{QB} = \frac13V_0$$ $$���̒��̓d�ʍ��O�Ȃ̂ŁAV_P = V_0 - V_{AP} = V_Q = V_{QB} = \frac13V_0 �BAns�i�S�j$$ $$$$ $$$$ $$$$
�����̃R���f���T����ł������ꍇ�̍����Ód�e�ʂ̌v�Z���@�B�����̏ꍇ����ڑ��ƕ���ڑ��̕����^�Ȃ̂ŁA���ꂼ��̌v�Z���@���킩���Ă���Α����̓d�C��H�̍����Ód�e�ʂ��v�Z�ł���B������R�̎��ƈႤ�̂Œ��ӂ��K�v�B
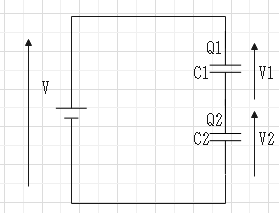
�ǂ̃R���f���T�ɂ������d�ׂ����܂�B�d���͐Ód�e�ʂɉ����ĕ��z�����B�����Ód�e�ʂ̋t���͊e�R���f���T�̐Ód�e�ʂ̋t���̘a�ŕ\�����B
$$�u���u_1�{�u_2�B�p���p_1���p_2�B�u_1��\frac{�p}{�b_1} = \frac{C_2}{C_1 + C_2}V�A�u_2��\frac{�p}{�b_2} = \frac{C_1}{C_1 + C_2}V�B$$
$$\frac{�P}{�b}��\frac{�P}{�b_1}�{\frac{�P}{�b_2}�A�b��\frac{�b_1 �b_2}{�b_1�{�b_2}$$
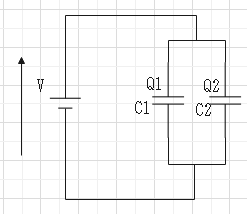
��̃R���f���T�ɂ�����d���͈ꏏ�B�d�ׂ͐Ód�e�ʂɂ���Č��܂�B�����Ód�e�ʂ͊e�R���f���T�̐Ód�e�ʂ̘a�B
$$�p_1���b_1 �u�A�p_2���b_2 �u�B�p���p_1�{�p_2 �A�b���b_1 �{�b_2 $$

$$����ڑ��̍����e��\frac{2C^2}{C+2C} = \frac23C$$ $$�Ód�G�l���M�[\frac12\frac23C {V_1}^2$$ $$����ڑ��̍����e��3C$$ $$�Ód�G�l���M�[\frac123C{V_2}^2$$ $$���҂̐Ód�G�l���M�[���������̂�\frac13{V_1}^2 = \frac32{V_2}^2$$ $$V_1 = \frac{3}{\sqrt 2}V_2$$ $$V_c = \frac23 V_1 ���@|\frac{V_c}{V_2}| = \sqrt2$$

$$�}�P��Q_1 = Q_2 V_1 = \frac{2}{4+2}6V = 2V,Q_1 = 2 \times 4 = 8[\mu C]$$ $$�}�Q��Q_1 + Q_2 = 16[\mu C] V_1 = V_2,\frac{2}{2+4}Q_1 = \frac{4}{2+4}Q_2��� Q_1 = 16 \div \frac{3}{2} = \frac[32][3]$$ $$V = \frac{32}{3} \div 4 = \frac{8}{3} Ans�i�R�j$$ $$$$ $$$$ $$$$ $$$$
�d�C��H[����]/ �d���C�w/ �d�C��H[��]/ �d�C��H[�O����]/ �d�q��H
�Ȋw�̕���[�H�w�E���w]