電気回路[直流]/ 電磁気学/ 電気回路[交流]/ 電気回路[三相交流]/ 電子回路
科学の部屋[工学・化学]
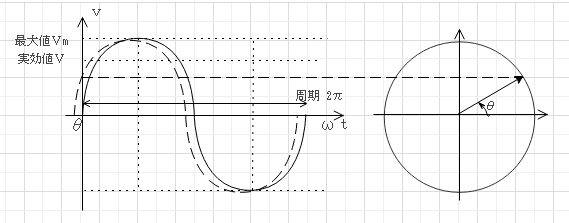
$$v=V_m \sin(\omega t +\theta ) フェーザ(ベクトル)表現:V = Vm∠\theta$$
$$v:瞬時値[V] V_m:最大値、振幅$$
$$\omega:角速度、角周波数[rad/s]$$
$$\theta :初期位相角[rad]$$
$$T=\frac{2\pi}{\omega} :周期[s],周波数f=\frac{1}{T}[Hz]$$
$$実効値V=\root \of{\frac1T \int^T_0 v^2 dt}=\frac{V_m}{\root \of2}$$
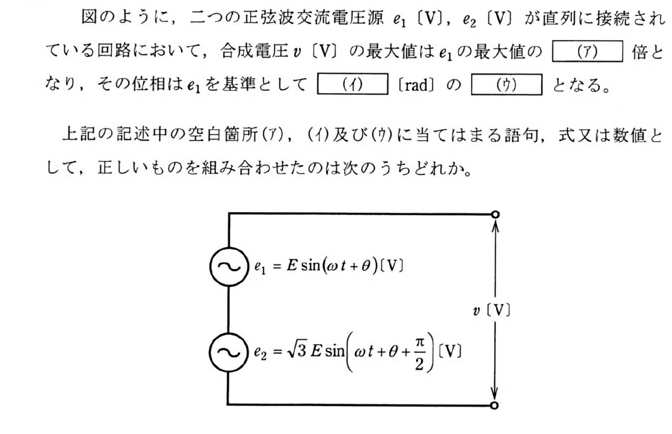

$$[\sin{(\alpha + \beta)} = \sin{\alpha} \cos{\beta} + \cos{\alpha}sin{\beta}]$$ $$T = \omega t + \theta と置くとe_1 + e_2 = E\{ \sin{T} + \sqrt{3} \sin{{T} + \frac{\pi}{2}}\}$$ $$= E\{ \sin{T} + \sqrt{3} (\sin{T} \cos{\frac{\pi}{2}} + \cos{T}sin{\frac{\pi}{2}})\}$$ $$= 2E\{ \frac{1}{2}\sin{T} + \frac{\sqrt{3}}{2} \cos{T}\}$$ $$= 2E\{ \cos{\frac{\pi}{3}}\sin{T} + \sin{\frac{\pi}{3}} \cos{T}\} $$ $$= 2E \sin{(\omega t + \theta + \frac{\pi}{3})}$$ $$または、$$ $$e_2はe_1より位相が\frac{\pi}{2}進んでいて、大きさは\sqrt{3}倍なので$$ $$E_1= E, E_2 = j\sqrt{3}E$$ $$E_1 + E_2の大きさは\sqrt{1^2 + (\sqrt{3})^2} = 2$$ $$E_1 + E_2の角度は\arctan{\sqrt{3}} = \frac{\pi}{3}$$ $$よってe_1 + e_2 =2E \sin{(\omega t + \theta + \frac{\pi}{3})}$$ Ans.(5)
コンデンサやコイルに流れる電流は電圧と位相がずれます。
$$V=ZI。 Z:インピーダンス[Ω]$$
$$\theta :電流と電圧の位相差[rad],j:複素数$$
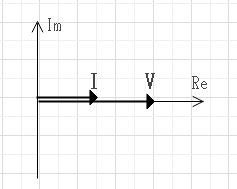
$$Z=R 。Z:抵抗値[Ω]$$
$$V=RI$$
$$\theta = 0$$
電流と電圧の位相差なし(同相)。
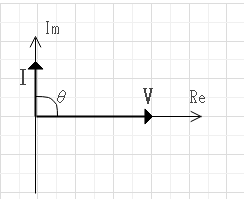
$$Z=\frac{1}{j\omega C}。C:静電容量[F] $$
$$V=\frac{I}{j\omega C} = -j\frac{I}{\omega C}$$
$$\theta = -\frac{\pi}{2}$$
コンデンサに流れる電流はそこにかかる電圧より位相がθほど遅れている。
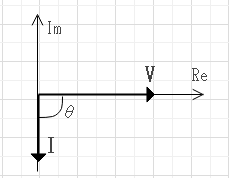
$$Z=j\omega L。L:インダクタンス[H]$$
$$V=j\omega L I$$
$$\theta = \frac{\pi}{2}$$
コイルに流れる電流はそこにかかる電圧より位相がθほど進んでいる。
$$Z=R+jX$$
R:レジスタンス(抵抗分)X:リアクタンス(コイルとコンデンサ分)X>0:誘導性、X<0:容量性
$$R=|Z| \cos\theta ,X=|Z|\sin\theta,\theta=\arctan{\frac{X}{R}}$$
$$P(t)=v(t)i(t)$$
電源から負荷Zへ供給される瞬時電力の平均値$$P=|V||I|\cos\theta = R I^2[W]$$
見かけの電力$$S=|V||I| [VA]$$
電圧と電流が直交する電力。平均すると0。電源と負荷との間のエネルギーのやり取り$$Q=|V||I|\sin\theta = X I^2 [var]$$
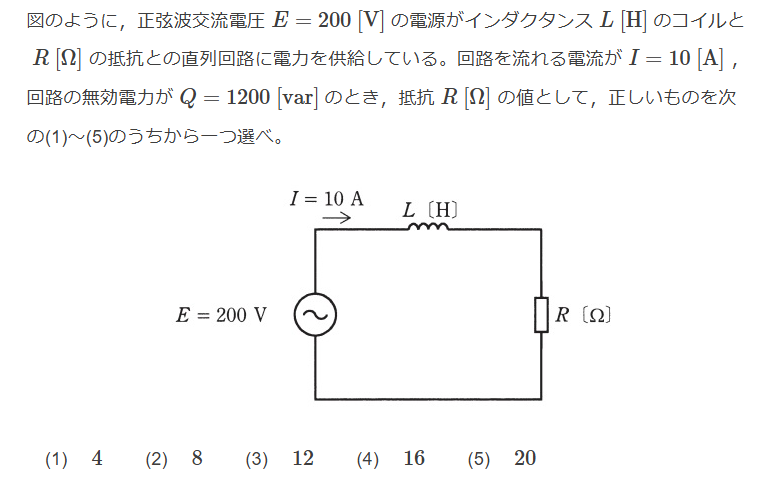
$$Q = 1200 = X I^2 = X 10^2 , X = 12$$ $$E = Z I = \sqrt{R^2 + X^2}I $$ $$200 = \sqrt{R^2 + 12^2}10$$ $$R = 16$$ $$Ans.(4)$$ $$$$
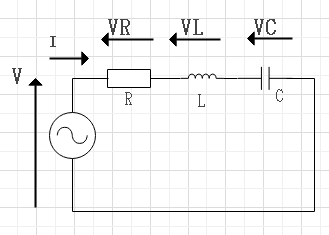
$$\bf{V} = \bf{V_R} + \bf{V_L} + \bf{V_C}。$$
$$Z=R+j(\omega L-\frac{1}{\omega C})$$
$$|Z|=\root \of{R^2+(\omega L-\frac{1}{\omega C})^2}$$
電流が最大の場合はインピーダンスが最小の時。つまりリアクタンスが0。
$$|Z|_{min}=R,\omega L-\frac{1}{\omega C}=0$$
リアクタンスが0時を共振状態という。その時の周波数を共振周波数という。
$$\omega_0 = \frac{1}{\root \of{LC}}$$
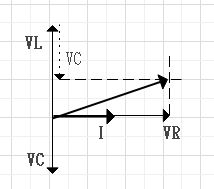
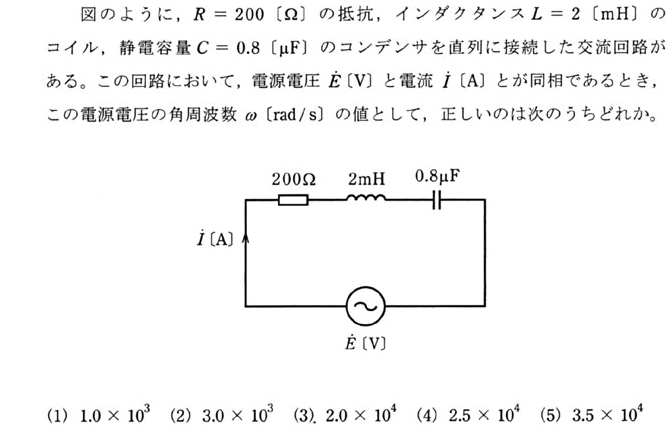
$$電源電圧と電流が同相:V_CとV_Lの和が0、リアクタンスが0の時。$$ $$その時の周波数は共振周波数。$$ $$\omega = \frac{1}{\root \of{LC}} = \frac{1}{\root \of{2 \times 10^{-3} \times 0.8 \times 10^{-6}}}$$ $$= 2.5 \times 10^4 [rad/s] $$ $$Ans.(4)$$ $$$$
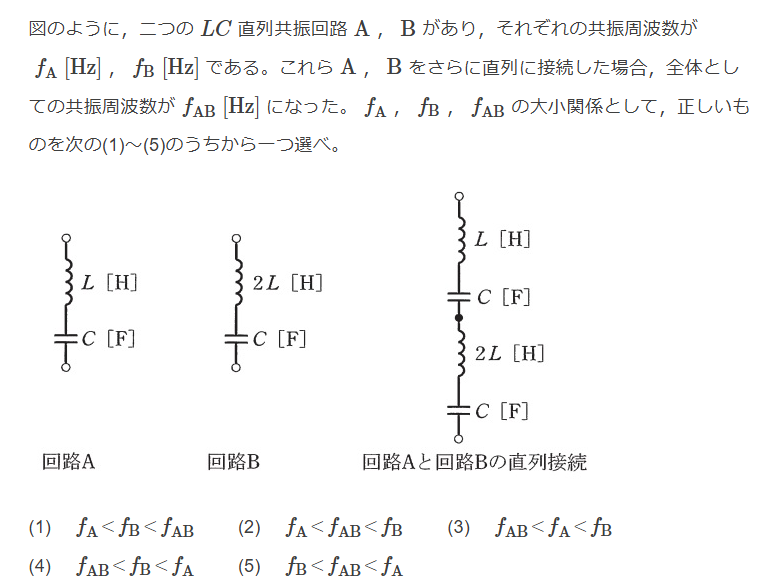
$$共振周波数 f_0 = \frac{\omega_0 }{2 \pi }$$ $$回路A f_A = \frac{1}{2 \pi \root \of{LC}}$$ $$回路B f_B = \frac{1}{2 \pi \root \of{2LC}}$$ $$回路AB コイルの合成リアクタンスは3L, コンデンサの合成容量は\frac{C}{2}$$ $$f_{AB} = \frac{1}{2 \pi \root \of{\frac{3}{2}LC}}$$ $$よってf_A>f_{AB}>f_B 。Ans.(5)$$
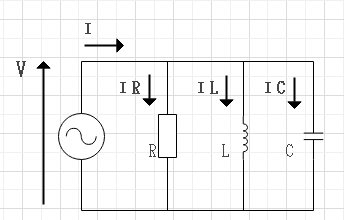
$$\bf{I} = \bf{I_R} + \bf{I_L} + \bf{I_C}。$$
$$\frac{1}{Z}=\frac1R +j(\omega C-\frac{1}{\omega L})$$
$$Z=\frac{1}{\frac1R +j(\omega C-\frac{1}{\omega L})}$$
$$|Z|=\root \of{\frac{1}{\frac1R^2 +(\omega C-\frac{1}{\omega L})^2}}$$
電流が最大の場合はインピーダンスが最小の時。つまりリアクタンスが0。
$$|Z|_{min}=R,\omega C-\frac{1}{\omega L}=0$$
リアクタンスが0時を共振状態という。その時の周波数を共振周波数という。
$$\omega_0 = \frac{1}{\root \of{LC}}$$
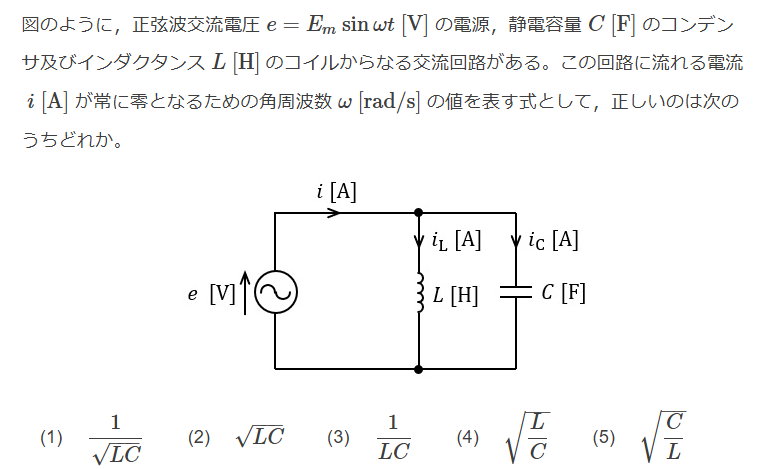
$$ i_L = - j\frac{e}{\omega L} , i_C = j \omega C e$$ $$i = i_L + i_C = j(\omega C - \frac{1}{\omega L}) =0 ,\omega = \frac{1}{LC}$$ $$Ans.(1)$$ $$$$
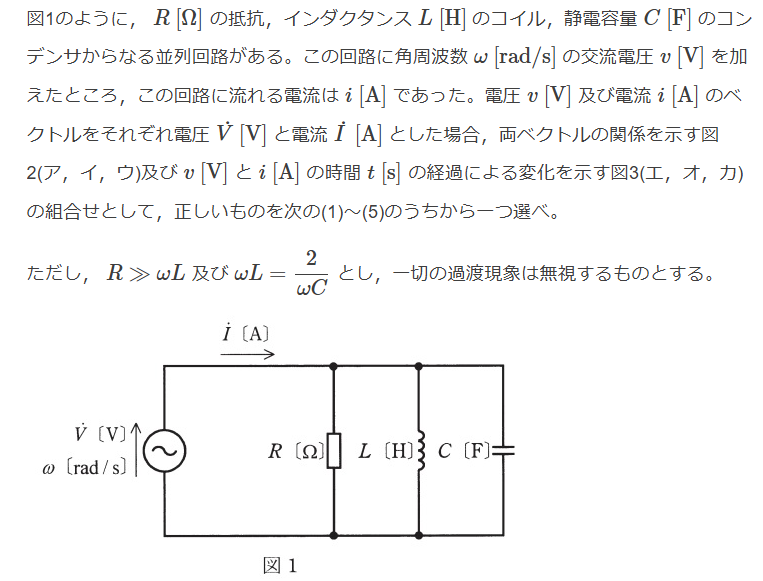
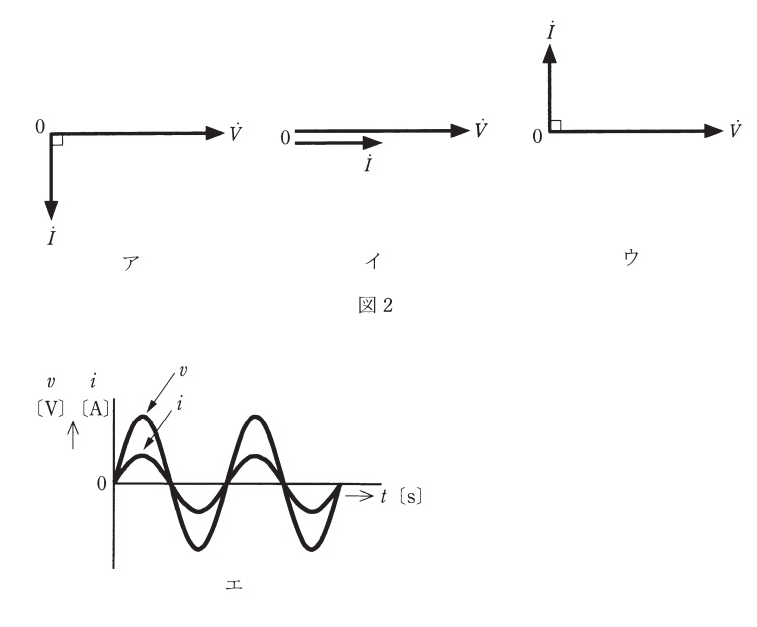
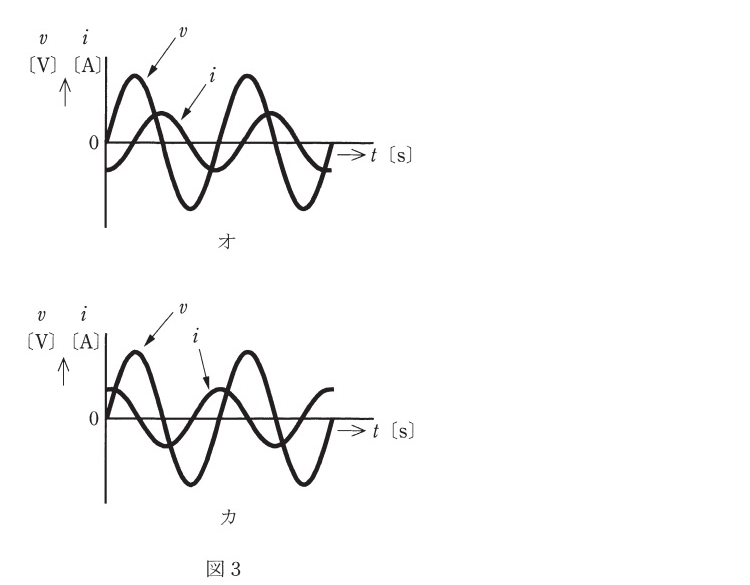

$$I = \frac{V}{R} = V\{\frac1R +j(\omega C-\frac{1}{\omega L})\}$$ $$R = \omega L \omega L = \frac{2}{\omega C} より$$ $$Rは無視できて、\frac{1}{R} = j(\omega C-\frac{1}{\omega L}) = \frac{j}{2}\omega C$$ $$よって電流は電圧よりも\frac{\pi}{2}進んでいる。$$ $$Ans.(5)$$ $$$$ $$$$ $$$$
電気回路[直流]/ 電磁気学/ 電気回路[交流]/ 電気回路[三相交流]/ 電子回路
科学の部屋[工学・化学]