電気回路[直流]/ 電磁気学/ 電気回路[交流]/ 電気回路[三相交流]/ 電子回路
科学の部屋[工学・化学]
$$三相交流とは、$$$$電流または電圧の位相を互いに120°(\frac{2\pi}3)$$$$ずらした3系統の単相交流を組み合わせた交流である$$
電源の電圧電流が対称ならその電源を平衡三相電源、負荷が対称なら平衡負荷という。平衡三相電源に平衡三相負荷が接続されている回路を平衡(対称)三相回路という。
$$E_a,E_b,E_C:電源電圧。$$$$V_{ab}:線間電圧。V_a:相電圧。$$$$I_{ab}:相電流。I_a:線間電流。$$$$Z_a,Z_b,Z_c:負荷。\cos \theta:Z_aの力率$$
一相の電力の3倍。
$$P = 3 V_a I_a \cos \theta = \root \of 3 V_{ab}I_{ab} \cos \theta $$
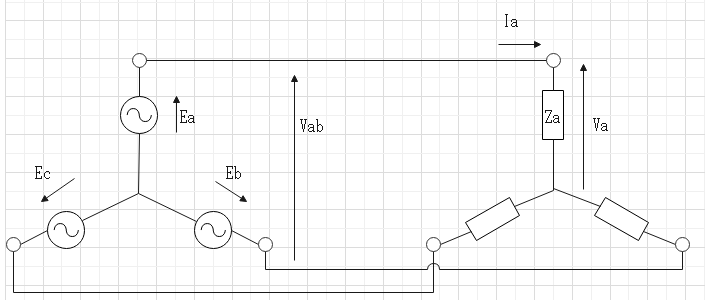
$$線間電圧V_{ab}=E_a-E_b。$$ $$ベクトルの引き算になるので線間電圧は相電源電圧E_aの\root \of3倍、位相が30°進み。$$
$$E_a = \frac{1}{\root \of3}V_{ab} = V_a$$
$$I_a=\frac{V_a}{Z_a}$$
$$三相の電力P = 3 V_a I_a = \root \of3 V_{ab}I_a :単相の電力の3倍$$

$$(1)○$$ $$(2)○$$ $$(3)○$$ $$(4)× P=\root \of3 V_l I_l = 3 V_p I_p$$ $$(5)○$$ $$$$
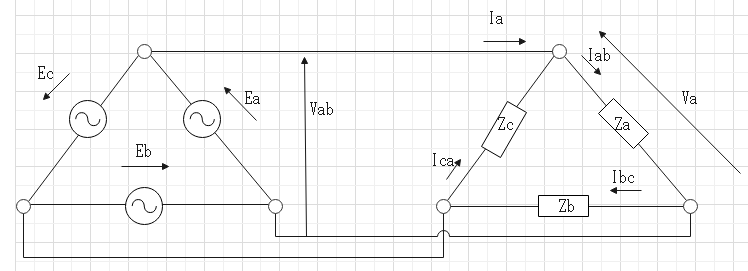
$$相電流I_{ab}=I_a-I_b$$ $$ベクトルの引き算になるので線電流は相電流の\root \of3倍、位相が30°遅れ。$$
$$E_a = V_{ab} = V_a$$
$$I_a = \root \of3 I_{ab} $$
$$I_{ab}=\frac{V_a}{Z_a}$$
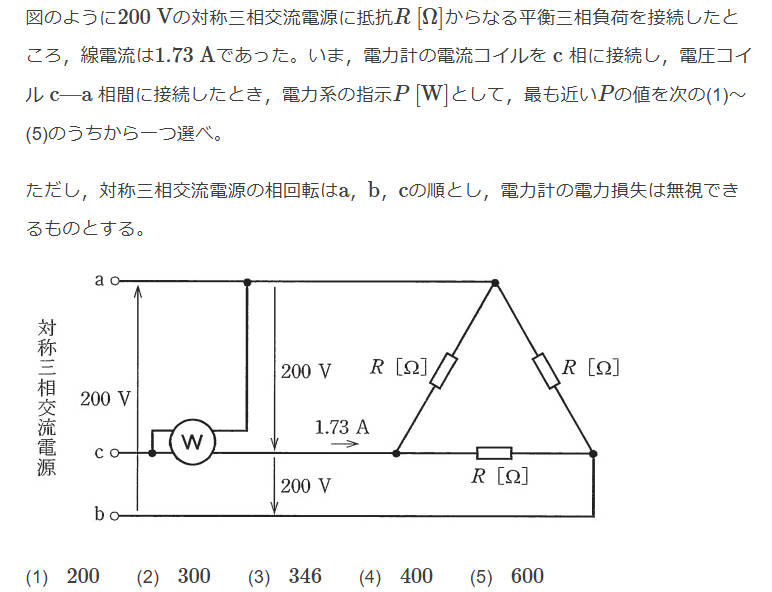
$$電力計の値は線間電圧・線電流・電圧と電流の位相差できまる$$ $$線間電圧200[V],線電流1.73[A], $$ $$線間電圧(=相電圧)と相電流が同相。なので線間電圧と線電流の位相差30°$$ $$P=200 \times 1.73 \ttimes \cos{30°} \fallingdotseq 300 Ans.(2)$$ $$別の相に単相電力計を接続し二つの測定値の和が三相電力になる$$

$$極性を変えた電力計の値はマイナスにする$$ $$P = 490 - 25 = 465$$ $$Ans.(3)$$ $$$$
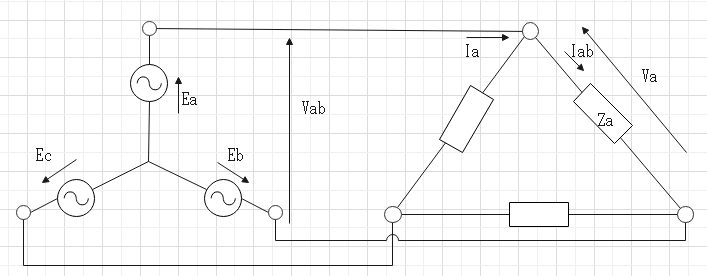
$$E_a = \frac{1}{\root \of3}V_{ab} = \frac{1}{\root \of3}V_a$$
$$I_a = \root \of3 I_{ab} $$
$$I_{ab}=\frac{V_a}{Z_a}$$
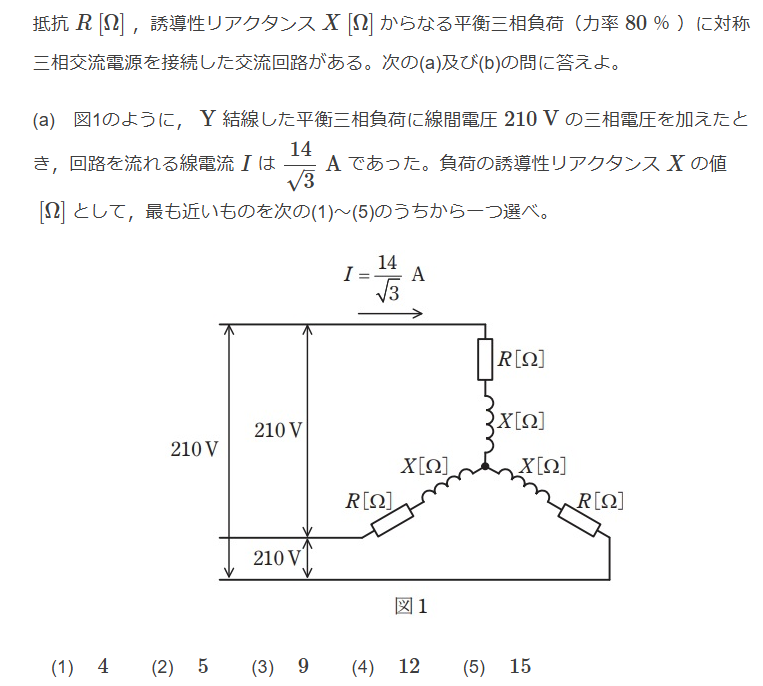
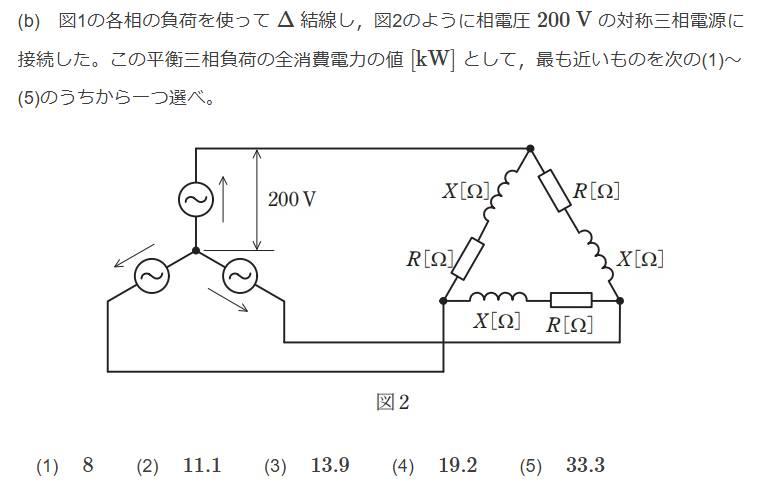
(a)$$Y結線した負荷にかかる電圧は\frac{210}{\root \of 3}$$ $$|Z| = \frac{210}{\root \of 3}÷\frac{14}{\root \of 3} = 15$$ $$\cos{\theta} = 0.8よりX = 9$$ $$Ans.(3)$$ (b)$$負荷をΔ→Y変換するとインピーダンスは\frac{Z}{3} = 5$$ $$R = 4$$ $$I = \frac{200}{5} =40$$ $$三相当たりの消費電力は$$ $$P = 3 R I^2 = 19.2 [kW]$$ $$Ans.(4)$$
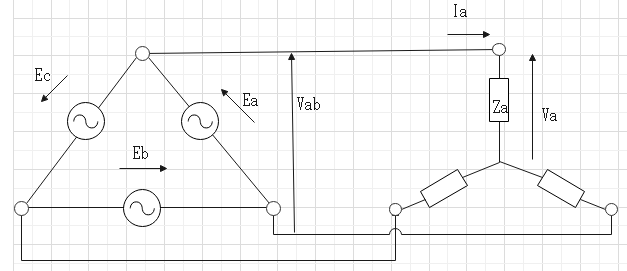
$$E_a = V_{ab} = \root \of3V_a$$
$$I_{a}=\frac{V_a}{Z_a}$$

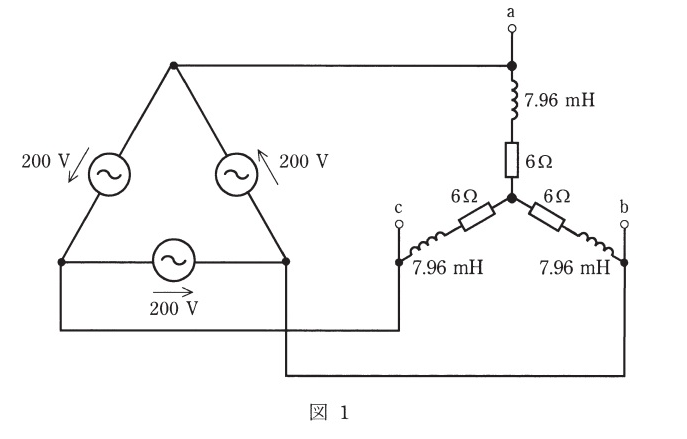
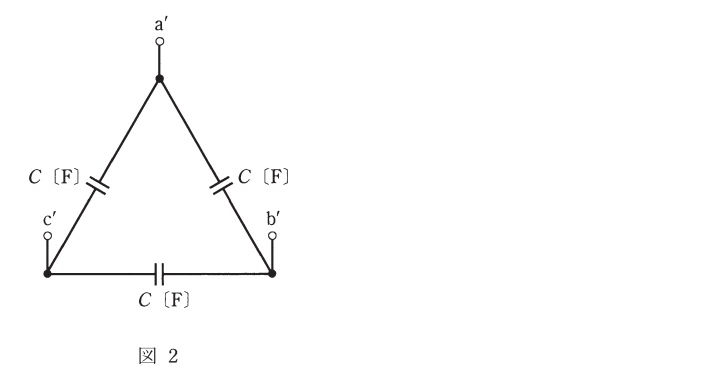
(a)$$負荷にかかる相電圧は\frac{200}{\root \of 3}$$ $$インピーダンスの大きさは\root \of{R^2 + (\omega L)^2}$$ $$=\root \of{6^2 + (2 \pi \times 50 \times 7.96 \times 10^{-3})^2} = 6.5$$ $$P = 3RI^2 = 3 R \times (\frac{相電圧}{Z})^2$$ $$= 3 \times 6 \times \frac{(\frac{200}{\root \of 3})}{6.5}^3 = 5680$$
$$Ans.(4)$$ (b)$$Δ→Y変換したコンデンサのインピーダンスは\frac{1}{j3\omega C}Z$$ $$コンデンサを並列接続した合成インピーダンスは$$ $$Z=\frac{(R + j \omega L) \times -j\frac{1}{3 \omega C}}{(R + j \omega L) -j\frac{1}{3 \omega C}}$$ $$= \frac{\frac{\omega L}{3 \omega C}-jR\frac{1}{3 \omega C}}{R + j (\omega L -\frac{1}{3 \omega C})} \times \frac{R - j (\omega L -\frac{1}{3 \omega C})}{R - j (\omega L -\frac{1}{3 \omega C})}$$ $$=\frac{R\frac{\omega L}{3 \omega C} + R\frac{1}{3 \omega C}(\omega L -\frac{1}{3 \omega C}) -j\{R^2 \frac{1}{3 \omega C}+\frac{\omega L}{3 \omega C}(\omega L - \frac{1}{3 \omega C})\}}{R^2 +(\omega L -\frac{1}{3 \omega C})^2}$$ $$力率1=虚数部が0なので$$ $$R^2 \frac{1}{3 \omega C}+\frac{\omega L}{3 \omega C}(\omega L - \frac{1}{3 \omega C} = 0$$ $$=\frac{1}{3 \omega C}(R^2 + \omega^2 L^2 - \frac{L}{3C})$$ $$C = \frac{L}{3(R^2 + \omega^2 L^2)}$$ $$= \frac{7.96 \times 10^{-3}}{3 \{6^2 + (2 \pi \times 50 \times 7.96 \times 10^{-3})^2\}}$$ $$= 6.28 \times 10^{-5}$$ $$Ans.(1)$$ $$$$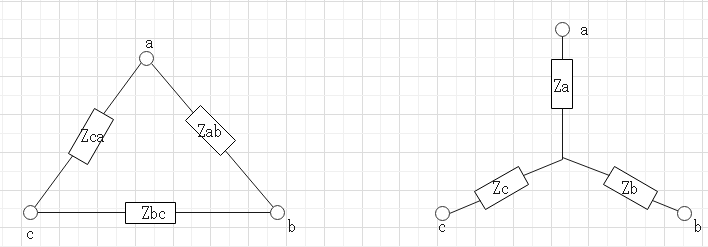
$$Z_a = \frac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}$$
$$Z_b = \frac{Z_{bc}Z_{ab}}{Z_{ab}+Z_{bc}+Z_{ca}}$$
$$Z_c = \frac{Z_{ca}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}$$
$$均等負荷Zの場合\frac13Z$$$$Z_{ab} = Z_a + Z_b + \frac{Z_a Z_b}{Z_c}$$
$$Z_{bc} = Z_b + Z_c + \frac{Z_b Z_c}{Z_a}$$
$$Z_{ca} = Z_c + Z_a + \frac{Z_c Z_a}{Z_b}$$
$$均等負荷Zの場合3Z$$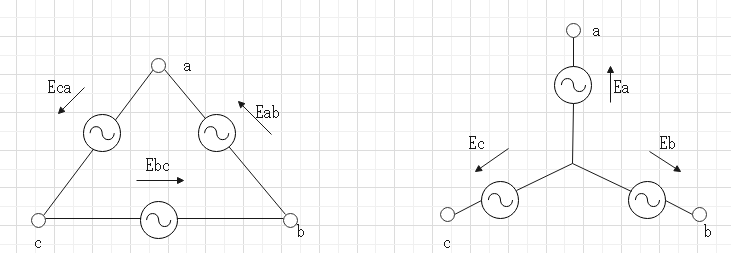
電気回路[直流]/ 電磁気学/ 電気回路[交流]/ 電気回路[三相交流]/ 電子回路
科学の部屋[工学・化学]