火力発電

熱力学

熱力学の第一法則

内部エネルギーの増加量は外部からくわえられた仕事と熱量の和に等しい。

$$dU = dQ +dW,dW = -PdV$$ $$U:内部エネルギー[J]、P:圧力[Pa]、W:仕事[J]、Q:熱量[J]、V:体積[m^3]$$

エンタルピーH

物体の内部エネルギーUと圧力エネルギーPVの和。流体が持つ熱力学エネルギー $$H = U + PV $$

$$H:エンタルピー[J]$$

エントロピーS

増減した熱量とその時の温度の比率 $$dS = \frac{dQ}{T}$$

$$H:エントロピー[J/K],T:温度[K],Q:熱量[J]$$

ボイル＝シャルルの法則

$$\frac{P_1 V_1}{T_1} = \frac{P_2 V_2}{T_2}$$ $$P:圧力[Pa]、V:体積[m^3]、T:温度[K]$$

理想気体の状態方程式

$$P V = n R T$$

気体の状態変化

等温変化

$$dT =0, dU = 0,dQ = dW$$

$$$$

等容（等積）変化

$$dV = 0,dQ = dU$$

$$$$

等圧変化

$$dP = 0, dQ = dH$$

$$$$

断熱変化

$$dQ = 0,dU +dW = 0$$

$$$$

カルノーサイクル

フランスの物理学者カルノーの考えた、温度の異なる2つの熱源の間で動作する可逆な熱力学サイクルの一種。熱機関の熱効率が最大になる理想サイクル。蒸気などが、異なる温度間を等温膨張・断熱膨張・等温圧縮・断熱圧縮の4行程で循環。熱の出入りがある時のみ熱交換が行われ、他の状態は断熱されている。

等温膨張（1-2）

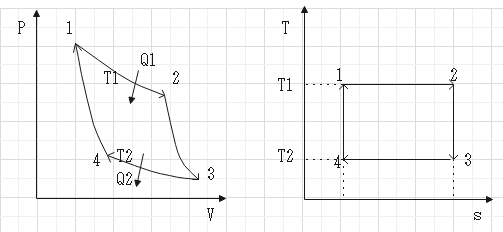
熱が流入して、等温状態で体積が膨張します。

$$U_{12} = 0,Q_1 = W_1 = \int^{V_2}_{V_1}PdV $$

断熱膨張（2-3）

断熱状態で、体積が膨張し温度が低下します。

$$Q_{23} = 0,U_{23} = -W_2 = -\int^{V_3}_{V_2}PdV$$

等温圧縮（3-4）

熱が流出して、等温状態で体積が圧縮します。

$$U_34 = 0,Q_2 = W_3 = \int^{V_4}_{V_3}PdV$$

断熱圧縮（4-1）

断熱状態で、体積が圧縮し温度が上昇します。

$$Q_{41} = 0,U_{41} = -W_4 = -\int^{V_1}_{V_4}PdV$$

汽力発電

水蒸気でタービン発電機を回し、電力変換する発電方法

電気集じん器は粒子を負イオンに帯電させて、分離除去する。

Ans.(4)

Ans.(3)

ボイラ内の蒸気圧力が一定限度を超えたとき，蒸気を放出させる弁は安全弁。蒸気加減弁はタービン入口の蒸気量を制御し、出力を調整する。

Ans.(4)

ランキンサイクル

カルノーサイクルの等温変化を等圧変化にかえたもの。汽力発電を表現できる基本的な熱力学サイクル。

給水ポンプ（1-2）

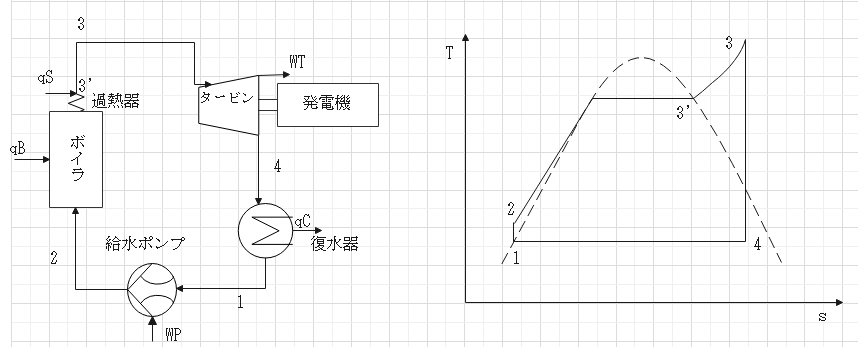
断熱（等エントロピー）圧縮

飽和水（その圧力で沸点の温度（飽和温度）の水）を断熱圧縮。

ボイラ（2-3'）

等圧加熱

飽和水を等圧加熱し飽和蒸気になる。飽和蒸気線（点線）の内側では水分を含んた湿り蒸気。点3'で水分のない乾燥飽和蒸気。

過熱器（3'-3）

等圧加熱

乾燥飽和蒸気を等圧加熱し過熱蒸気（飽和温度より過熱された蒸気）になる。

タービン（3-4）

断熱（等エントロピー）膨張

過熱蒸気を断熱膨張し湿り蒸気になる。

復水器（4-1）

等圧冷却

湿り蒸気は等圧冷却され飽和水になる。

給水ポンプは断熱圧縮

Ans.(1)

再熱サイクル

タービン系の途中から蒸気を取り出し、ボイラの再熱器へ送り、再加熱の工程を加えたもの。

再生サイクル

タービン内の蒸気を膨張途中から抽出して給水加熱器に送りボイラ給水を加熱。

再熱再生サイクル

湿り蒸気によるタービンの内部損失を減少させる再熱サイクルと復水器で放出される熱量を回収する再生サイクルを組み合わせたもの。

再熱サイクルはタービンで膨張した湿り蒸気をボイラの再熱器で加熱し，再びタービンに送って膨張させる熱サイクル。

Ans.(4)

火力発電設備

ボイラ

自然循環ボイラ

自然の浮力によって蒸発管と炉外の降水管との間で水の循環

強制循環ボイラ

降水管途中に設けた循環ポンプによって強制的に循環能力を高める

貫流ボイラ

ボイラドラムなし、蒸発管内で蒸気発生

コンパインドサーキュレーションボイラ

強制循環と貫流のの長所の組み合わせ

コンバインドサイクル発電は起動・停止が容易で、時間も短い

Ans.(2)

排熱回収方式のコンバインドサイクル発電は、ガスタービンで発電した後，高温の排気を排熱回収ボイラで熱回収し，その蒸気を蒸気タービンで発電する方式

$$コンバインドサイクル発電の熱効率\eta = \frac{ガスタービン機械的出力　＋　蒸気タービン機械的出力}{ガスタービン入力Q_g}$$ $$\eta_g :ガスタービン発電熱効率、\eta_s :蒸気タービン発電熱効率$$ $$\eta = \frac{Q_g \eta_g + \eta_s (Q_g - Q_g \eta_g)}{Q_g}$$ $$= \eta_g + (1 - \eta_g) \eta_s$$ $$\eta_g = \frac{\eta - \eta_s}{1 - \eta_s}, \eta_s = \frac{\eta - \eta_g}{1 - \eta_g}$$ $$\eta_g = \frac{0.48 - 0.2}{1 - 0.2} = 0.35$$ Ans.(4)

ボイラ設備

空気予熱器

排ガスでボイラに入る前の空気を温め熱効率を上げる。

節炭器

排ガスでボイラに入る前の給水を温め熱効率を上げる。

過熱器

ボイラから出た飽和蒸気をタービンに入る前に再過熱する。

再熱器

タービンの高圧側の排気を再加熱してタービンの低圧側に送る。

節炭器は蒸気ではなく排ガス（燃焼ガス）によってボイラ給水を加熱する。

Ans.(4)

復水器
低圧タービンなどから排出される蒸気を冷却し、純粋な水として復水させる。復水ポンプ、抽気ポンプ、復水脱塩装置、循環水ポンプ

復水器の真空度が高いとタービン出口の圧力が下がり、入り口との圧力差が大きくなり、タービンの出力が上がる。

Ans.(4)

給水系統

復水昇圧ポンプ、低圧給水加熱器、脱気器、高圧給水ポンプ、高圧給水加熱器

燃焼空気量

理論酸素量

$$Ｏ_o = \frac{C}{12}+\frac{H}{4}+\frac{S}{32}-\frac{O}{32}[kmol/kg]$$ $$C:燃料１�s当たりの炭素の量[kg],H:水素の量,S:硫黄の量,O:酸素の量$$

理論空気量

$$Ａ_o = \frac{22.4 Ｏ_o}{0.21}[Nm^3/kg]$$

空気比（空気過剰率）

$$\lambda　= \frac{Ａ（実際空気量）}{Ａ_o（理論空気量）}$$

$$(a) [W] = [J/s],[kW h] = 3600[kJ]$$ $$W（ワット）は一秒あたりのエネルギー[J]なので、一時間当たりなら3600を掛ける$$ $$一時間当たりの燃料[kg] = \frac{[kJh]}{[kJ/kg]}$$ $$=\frac{500 \times 10^3 \times 3600}{44000 \times 0.4} = 102273 = 102[t]$$ Ans.(5) $$(b)理論空気量[Nm^3] = \frac{22.4}{0.21}\times 燃料重量[kg] \times (\frac{0.85}{12}+\frac{0.15}{4})$$ $$= \frac{22.4}{0.21}\times 102273 \times (\frac{0.85}{12}+\frac{0.15}{4})$$ $$= 1181818 $$

Ans.(4)

$$(a)発電機効率 \eta　$$ $$9.3 \times 10^3 \times 10^3 = \frac{45000 \times 10^3 \times 3600}{44000 \times \eta}$$ $$\eta = \frac{45000 \times 10^3 \times 3600}{9.3 \times 10^3 \times 44000} = 0.396$$ Ans.(3) $$(b)重油の質量　\frac{600 \times 10^3 \times 24 \times 3600}{44000 \times 0.4} = 2945455[kg]$$ $$重油内の炭素の量　2945455 \times 0.85 = 2503636$$ $$C+O_2→CO_2 より重油内の炭素と発生する二酸化炭素の数は同じ$$ $$炭素の分子量12、二酸化炭素の分子量44より$$ $$二酸化炭素の量　2503636 \times \frac{44}{12} = 9810000[kg] = 9810[t]$$ Ans.(4)

$$(a)44000 \times 10^3 = \frac{600 \times 10^3 \times 0..95 \times 3600 \times 24}{26400 \times \eta}$$ $$\eta = \frac{600 \times 10^3 \times 0..95 \times 3600 \times 24}{26400 \times 44000 \times 10^3}$$ $$= 0.424$$ Ans.(3)
(b)所内率とは、発電所内で消費する電力が発電した電力のうちどれくらいの割合を占めているかを示す値。本問では無関係。 $$送電端効率 = 発電端効率（1-所内率）$$ $$発電端効率　= 発電機効率 \times タービン効率 \times ボイラ効率$$ $$\eta = \frac{0.40}{0.99 \times 0.45} = 0.898$$ Ans.(4)

$$(a)40 \times 10^3 = \frac{P \times 10^3 \times 3600}{44000 \times 0.38}$$ $$P = \frac{40 \times 10^3 \times 44000 \times 0.38}{10^3 \times 3600}= 185.78$$ Ans.(1) $$(b)タービン熱消費率=\frac{タービン入力熱量-復水器出口給水熱量[kJ/h]}{発電機端電力[kW]}$$ $$タービン入力熱量[kJ/h]=タービン熱消費率\times \frac{発生電力量}{発電効率}$$ $$タービン出力熱量[kJ/h]=3600 \times \frac{発生電力量}{発電効率}$$ $$復水器入力熱量[kJ/h] = タービン入力熱量-タービン出力熱量$$ $$=(8000 - 3600) \times \frac{185.78 \times 10^3}{0.98}$$ $$=834114286$$ $$復水器の放熱量[kJ/h]$$ $$=比熱 \times 水の密度 \times 流量 \times 温度上昇 \times 3600$$ $$復水器入力熱量 = 復水器の放熱量　より$$ $$834114286 = 4.0 \times 1.0 \times 10^3 \times 流量 \times 7 \times 3600$$ $$流量 = \frac{834114286}{4.0 \times 1.0 \times 10^3 \times 7 \times 3600} = 8.27$$ Ans.(2)