変電所

変圧器

重負荷には電力用コンデンサ、軽負荷時には分路リアクトル。

Ans.(4)

154kV以下は接地方式か消弧リアクトル接地方式が用いられている。22-154kVケーブル系統では補償リアクトル接地か低抵抗接地方式が用いられている。高圧配電系統では非接地式が用いられている。

Ans.(３)

変圧器の結線方式

Δ-Δ結線

$$\frac{線間電圧}{相電圧}:１,\frac{線電流}{相電流}:\root \of 3$$

Ｙ‐Ｙ‐Δ結線

$$\frac{線間電圧}{相電圧}:\root \of 3 ,\frac{線電流}{相電流}:１$$

Ｙ‐Δ結線

$$一次：\frac{線間電圧}{相電圧}:\root \of 3,\frac{線電流}{相電流}:１$$

$$二次：\frac{線間電圧}{相電圧}:１,\frac{線電流}{相電流}:\root \of 3$$

Δ‐Ｙ結線

$$一次：\frac{線間電圧}{相電圧}:１,\frac{線電流}{相電流}:\root \of 3$$

$$二次：\frac{線間電圧}{相電圧}:\root \of 3,\frac{線電流}{相電流}:１$$

Ｖ‐Ｖ結線

$$\frac{線間電圧}{相電圧}:１,\frac{線電流}{相電流}:\root \of 3$$

Ans.（２）

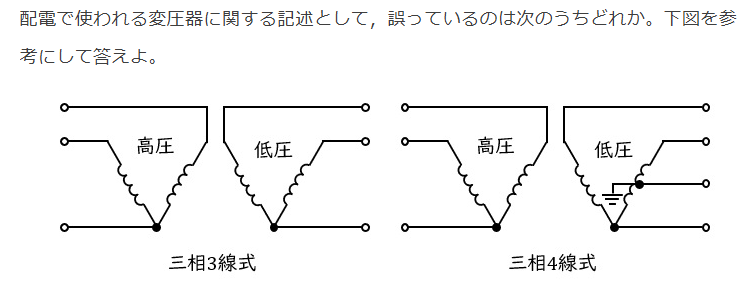
三相 4 線式（ V 結線）の変圧器容量の選定は，異容量の単相変圧器(異容量V結線)を組み合わせることが多い

Ans.（3）

Ans.（１）

（２）一次、二次ともにY結線なので、中性点接地できる。

Ans.（2）

変圧器の並列運転

負荷に供給した電力が一台の変圧器の容量で不足する場合、複数台の変圧器の一次側が二次側を並列接続し得て運転すること。

運転条件

電圧の極性が一致（三相器の場合は相回転の方向と角変位も）している

巻数比が等しく、一次二次の定格電圧が等しい

$$巻数比\alpha ：\frac{N_1}{N_2}=\frac{V_1}{V_2}=\frac{I_2}{I_1}$$

各変圧器の百分率インピーダンスが等しい

並行運転できる条件は， Y-Δ 同士，もしくは Y-Y 結線と Δ-Δ 結線の組み合わせのみ

Ans.（３）

単相変圧器の負荷分担

容量の異なる二台の単相変圧器を並行運転する場合の分散負荷。

$$P_a = P_l \frac{\% z_b \frac{P_{na}}{P_{nb}}}{\% z_a + \% z_b \frac{P_{na}}{P_{nb}}}$$

$$P_b = P_l \frac{\% z_a}{\% z_a + \% z_b \frac{P_{na}}{P_{nb}}}$$

$$P_a,P_b:二つ（A,B）の変圧器の分散負荷$$

$$z_a,z_b;一次に変換したインピーダンス$$

$$P_{na},P_{nb}:変圧器の定格容量、P_l:全負荷$$

$$$三相変圧器 TA の負荷分担 = 40 \times \frac{12.0\frac{80}{50}}{18.3 + 12.0\frac{80}{50}} = 20.48$ $$Ans.(3)$$ $$$$ $$$$ $$$$ $$$$

変圧器の等価回路

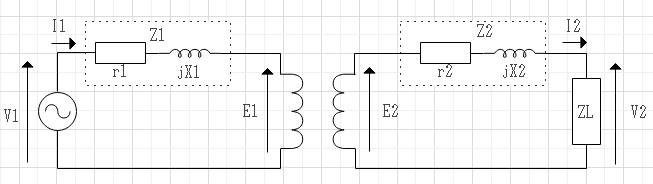
$$巻数比\alpha ：\frac{N_1}{N_2}=\frac{V_1}{V_2}=\frac{I_2}{I_1}$$

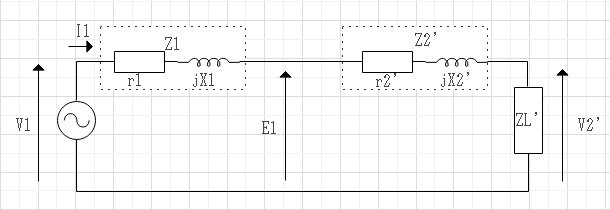
$$I_1 = \frac{I_2}{\alpha } ,E_1 = \alpha E_2,V'_2 = \alpha V_2,Z'_L = \alpha ^2 Z_L$$

$$Z'_2 = \alpha ^2 Z_2,r'_2 = \alpha ^2 r_2,X'_2 = \alpha ^2 X_2$$

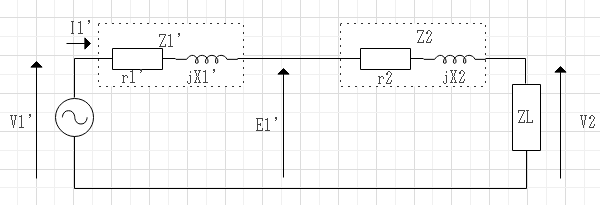
$$I'_1 = \alpha I_2 ,E'_1 = E_2 = \frac{E_1}{\alpha },V'_1 = \frac{V_1}{\alpha},I'_1 = \alpha I_2$$

$$Z'_1 = \frac{Z_1}{\alpha ^2},r'_1 = \frac{r_1}{\alpha },X'_1 = \frac{X_1}{\alpha }$$

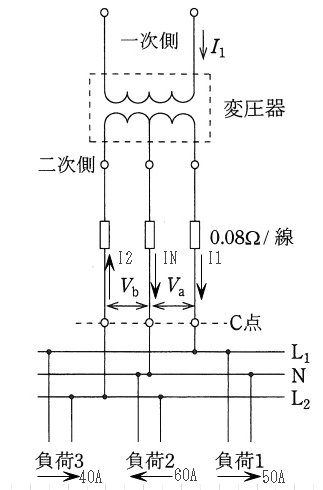
$$I_1 = 50 +40 = 90,I_2 = 40 + 60 = 100, I_N = 60-50 = 10$$ $$電線の電圧降下分は$$ $$V_1 = 90 \times 0.08 = 7.2, V_2 = 100 \times 0.08 = 8, V_N = 10 \times 0.08 = 0.8$$ $$V_a = 105 - V_1 + V_N = 98.6$$ $$V_b = 105 -V_N - V_2 = 96.2$$ $$一次側と二次側の電力は等しいので$$ $$6400 \times I_1 = 105 \times 90 + 105 \times 100$$ $$I_1 = 3.117[A]$$ $$Ans.(1)$$

百分率インピーダンス

全負荷電流（定格電流）下でのインピーダンス降下と相電圧の比

$$\%Z = \frac{IZ}{E}$$

電圧変動率ε

$$\varepsilon = \frac{無負荷二次電圧‐定格二次電圧}{定格二次電圧} = \%Z \cos \theta + \%X \sin \theta $$

$$\%Z = \frac{定格二次電流×二次側等価抵抗}{定格二次電圧}×100 = \frac{全負荷銅損}{定格容量}$$

$$\%X = \frac{定格二次電流×二次側等価リアクタンス}{定格二次電圧}$$

$$百分率リアクタンス　\%X = \frac{\root \of 3 \times 定格一次電流×一次側換算リアクタンス}{定格一次電圧}$$ $$= \frac{定格一次容量×一次側換算リアクタンス}{(定格一次電圧)^2}$$ $$= \frac{80 \times 10^6 \times 4.5}{(66 \times 10^3)^2} \times 100= 8.26[\%]$$ $$Ans.(3)$$ $$$$

変圧器の効率η

$$\eta = \frac{P_{out}}{P_{out} + P_{loss}}×100$$ $$= \frac{\alpha 定格出力}{\alpha 定格出力+鉄損 + \alpha ^2 銅損}$$ $$\alpha　：利用率$$

$$変圧器の効率が最大になる場合は、鉄損＝銅損$$

$$変圧器の効率が最大になる利用率は$$ $$250 = \alpha ^2 \times 1000$$ $$\alpha = 0.5$$ $$最大効率になるように調節した負荷は$$ $$50 \times 0.5 = 25[kW]$$ $$\eta = \frac{25 \times 10}{25 \times 10^3 + 250 + 250}×100$$ $$=98.0$$ $$Ans.(4)$$

全日効率

$$\eta _d = \frac{一日中の出力電力量}{一日中の出力電力量＋鉄損＋銅損}$$

開閉装置

ガス遮断器

六フッ化硫黄ガス（無色無臭、不活性・不燃・無毒）を使って電流を遮断、60[kV]以上の回路

真空遮断器

騒音小さい。77[kV]以下の回路

空気遮断器

遮断器に高圧の空気を吹きかけることで消弧するタイプ。11~500[kV]以下の回路

油遮断器

アーク放電のエネルギ→油をガス化→そのガスで消弧。騒音小さい、火災の危険

磁気遮断器

アーク電流の磁界を電磁石で消弧。

断路器

遮断器の端に設置、作業時などの回路に電流の流れていない状態での回路開閉

保護継電器

CTやVTの異常を認識し遮断器を作動

CT（変流器）：電流を小さくしその換算電流で管理

VT（変成器）：電圧異常を検知しやすいように計器の使いやすい電圧まで落とす

過電流継電器

CTから流れてきた電流が規定値以上の時に作動する継電器

過電圧継電器

VTの二次側の電圧が規定値を超えると作動する継電器

比率差動継電器

変圧器の一次側と二次側の両方にCTを置き、その両方の電流を測り電流比の異常があるとき作動

地絡継電器

変圧器の中性点が設置してある時地絡によって中性点に電流が流れるので、それをCTで検出。VTを接地させれば地絡時に二次側の電圧を検知。

地絡：電気回路とダイチが相対的に低いインピーダンスで電気的に接続される状態

零相変流器は，三相の電線を一括したものを一次側とし，3 線地絡事故などの不平衡電流が生じたときのみ二次側に電流が生じる機器。三相短絡事故や正常時には流れない

Ans.(5)

$$Ans.(3)$$

$$電流零点がないため，交流電流に比べ電流の遮断が困難$$ $$Ans.(5)$$

同調装置

電力用コンデンサ

重負荷により受電端の電圧が低下した際に進み無効電力を与えることで電圧を上昇させる

同期調相機

無負荷の同期電動機。励磁電流を加減することで進みor遅れ電流を流す

分路リアクトル

軽負荷により受電端の電圧が上昇した際に送れ無効電力を与えることで電圧を低下させる

静止型無効補償装置

高速で連続的に無効電力を調整できる調相設備。サイリスタ制御リアクトル方式、サイリスタ開閉コンデンサ方式、自励式インバータ方式。

$$Ans.(1)$$

三相短絡電流

百分率インピーダンス

基準インピーダンスに対して短絡インピーダンスが何％か $$\%Z = \frac{Z}{Z_{BASE}}$$ $$Z_{BASE} = \frac{{V_{BASE}}^2}{S_{BASE}}×100$$

$$S_{BASE}:基準容量,V_{BASE}:基準線間電圧,Z:短絡インピーダンス,Z_{BASE}:基準インピーダンス．$$

三相短絡電流

$$I_{3S} = \frac{100}{\%Z}I_{BASE}$$

$$I_{3S}:三相短絡電流,I_{BASE}:基準電流（定格電流）$$

三相短絡容量

$$S_S = \root \of 3 V_{BASE} I_{3S} = \root \of 3 V_{BASE} \frac{100}{\%Z}I_{BASE} = \frac{100}{\%Z} S_{BASE}$$

$$S_S:三相短絡容量$$

%Z直並列

%Zは容量に比例する。基準容量をそろえてインピーダンスと同じように直列と並列で合成できる。

$$負荷側から見た合成百分率インピーダンス = 1.5 + 18.3 = 19.8$$ $$二次側の短絡電流は$$ $$I_{3S} = \frac{100}{\%Z}I_{BASE}$$ $$= \frac{100}{\%Z} \times \frac{S_S}{\root \of 3 V_{BASE}} = \frac{100 \times 80}{ 19.8 \times \root \of 3 \times 11} = 21.2[kA]$$ $$遮断器の定格遮断電流は短絡電流よりも高い値を選ぶ。$$ $$Ans.(5)$$

$$(a)変圧器の二次側換算のインピーダンスは(\frac{22^2}{66^2})(0.018 + j 8.73) = 0.002 + j 0.97$$ $$短絡した線路のインピーダンスは0.5(0.2 + j 0.48) = 0.1 + j 0.24$$ $$変圧器と線路のインピーダンスは 0.102 + j 1.21$$ $$三相短絡電流は\frac{22000}{\root \of 3 \root \of {0.102^2 + 1.21^2}} = 10460[A]$$ $$Ans.(5)$$ $$(b)母線の線間電圧 = \root \of 3 \times 相電圧$$ $$相電圧は線路の電圧降下分。$$ $$よって線間電圧は \root \of 3 \root \of {0.1^2 + 0.24^2}\times 10460$$ $$= 4710[V]$$ $$Ans.(2)$$ $$$$ $$$$