水力発電/ 汽力発電/ 変電所/ 送電/ 原子力発電の仕組み
科学の部屋[工学・化学]
重力ダム
日本で一番多いダム。水の力をダムの重さで支える構造。断面は三角形。重い堤体を支えられる硬い地盤につくられる。
アーチダム
アーチ状の形をしたダム。重力ダムに比べて堤体が薄い。水の力をダムの両側や岩盤に分散させる構造のため、地盤が堅固な峡谷に適している。
バットレスダム
止水壁を扶壁(バットレス・控え壁)で支えるダム。
アースフィルダム
土を押し固めて作られたダム。最も古くからあり、世界最多のダム。
ロックフィルダム
岩石と土砂で作られたダム。ダム表面をコンクリートやアスファルトを敷いて水を通さないようにしているタイプもある。

大規模なアースダムに関しては安全性のために堤体内中心部に土質遮水壁(コア)を設ける場合もある。基礎の地質が強固の場合とは限らない。
Ans.(4)
水路式
河川の上流地点に取水ダムを設けて水をとりいれ、これを比較的長い水路により下流地点にある発電所に導いて、自然の落差を利用して発電。
ダム式
ダムにより皮をせき止めて水を貯え、これにより落差を得て発電。
ダム水路式
ダムにより落差を作り、水路によって利用する落差を大きくする発電。

純国産・再生可能エネルギーであり、蓄電・電力調整能力が高いため、役割は失われていない。
Ans.(3)
流込式
流量を調整する池を持たず河川の自然流量により発電。自流式。
貯水池式
貯水池により季節的な負荷変動に対応。
調整池式
貯水池式よりも調整能力は小さい。
揚水式
下部貯水池と上部貯水池を設け、軽負荷時に下池の水をポンプで上池に貯水。


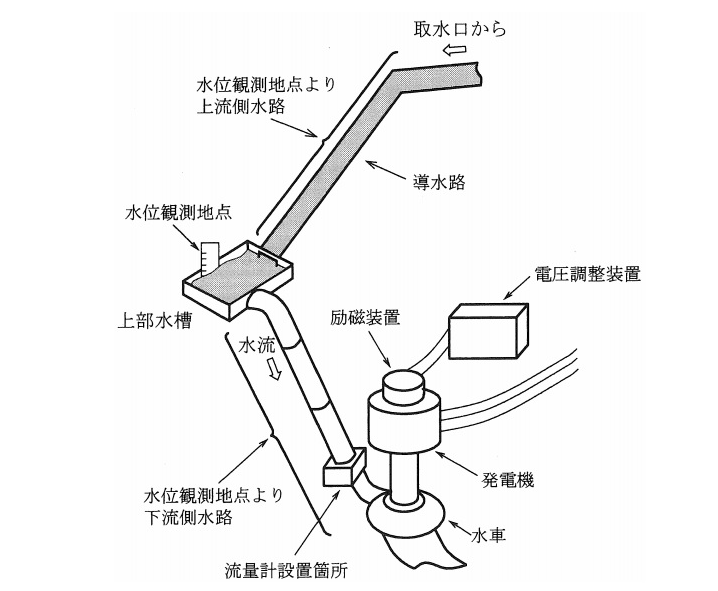
水位観測地点(上部水槽)より上流側水路:水車上流側の上部水槽で水位が上昇しているので×
水車を含む水位観測地点(上部水槽)より下流側水路:水車上流側の上部水槽で水位が上昇し、水車流量が低下したので○
電圧調整装置:発電機電圧はほとんど変化していないので×
励磁装置:有効電力出力が低下すると、誘導起電力が低下し、励起電圧も低下する×
発電機:保護リレーは動作していないので×
Ans.(2)
ペルトン水車
ノズルから噴出水をバケットに当ててランナ(羽根車)を回転させる。高落差用。ニードル弁で流量調整。デフレクターで水流をそらし水撃抑制。
フランシス水車
流水が半径方向にランナに充満して流入し、軸方向に向きを変えて流出。中高落差用。
斜流水車
ランナを通過する流量の流入方向は斜め。中落差用。
プロペラ水車
ランナを通過する流水の方向が軸方向。低落差用。

Ans.(5)

Ans.(5)

Ans.(4)
水頭
位置・圧力・速度エネルギーを位置エネルギーに換算。基準面に対する高さ。
$$H_1 + \frac{P}{\rho g} + \frac{v_1^2}{2 g} = H_2 + \frac{P}{\rho g} + \frac{v_2^2}{2 g} = 一定[m]$$
$$\rho :水の密度[kg/m^3] = 1000,g:重力加速度≒9.8$$ $$H_1,H_2:基準面からの高さ、v_1,v_2:平均流速$$ $$A_1,A_2:断面積、P_1,P_2:静水圧$$
$$A_1 v_1 = A_2 v_2 = 一定[m^3/s]$$
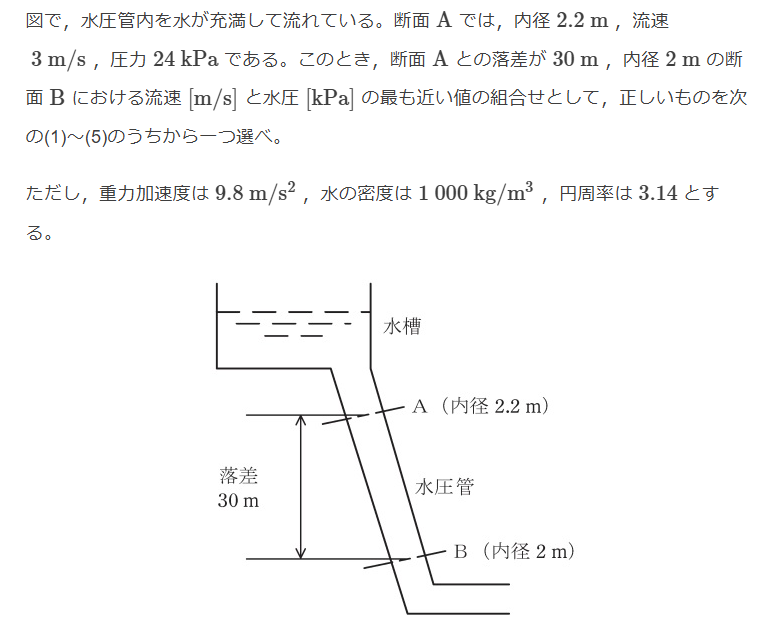

$$断面Bの流速V$$ $$\pi 1.1^2 \times 3 = \pi 1^2 \times V$$ $$V = 3.63$$ $$断面Bの水圧P$$ $$30 + \frac{24 \times 10^3}{1000 \times 9.8} + \frac{3^2}{2 \times 9.8} = 0 + \frac{P}{1000 \times 9.8} + \frac{3.63^2}{2 \times 9.8}$$ $$P = 1000 \times 9.8 ( 1000 \times 9.8 \times 30 + 24 \times 10^3 + 3^2 \times 500 - 3.63^2 \times 500)$$ $$ = 315911.55 = 315.9[kPa]$$ $$Ans.(3)$$
$$落差H[m]、流量Q:[m^3/s]$$
仕事率(工率),理論出力$$P_E = g \rho Q H = 9.8×1000QH[Nm/s] = 9.8 Q H [kW] $$
実際の発電所出力$$P_G = \eta _T \eta _G P_E = 9.8 \eta _T \eta _G Q H [kW]$$ $$\eta _T :水車効率、\eta _G:発電機効率$$
有効落差$$H = H_g - h_1 - h_2 - h_3 (反動水車の場合 -\frac{v^2}{2 g})$$ $$H_g:総落差、v:吹出し菅出口流速$$ $$h_1:導水路の損失、h_2:水圧管路の損失、h_3:放水路の損失$$

$$発電所出力は2500 \times 0.8 = 2000[kW]$$ $$P = 9.8 \eta _T \eta _G Q H $$ $$Q = \frac{P}{9.8 \eta _T \eta _G H}$$ $$= \frac{2000}{9.8 \times 0.92 \times 0.94 \times 100} = 2.36$$ $$$$ $$$$
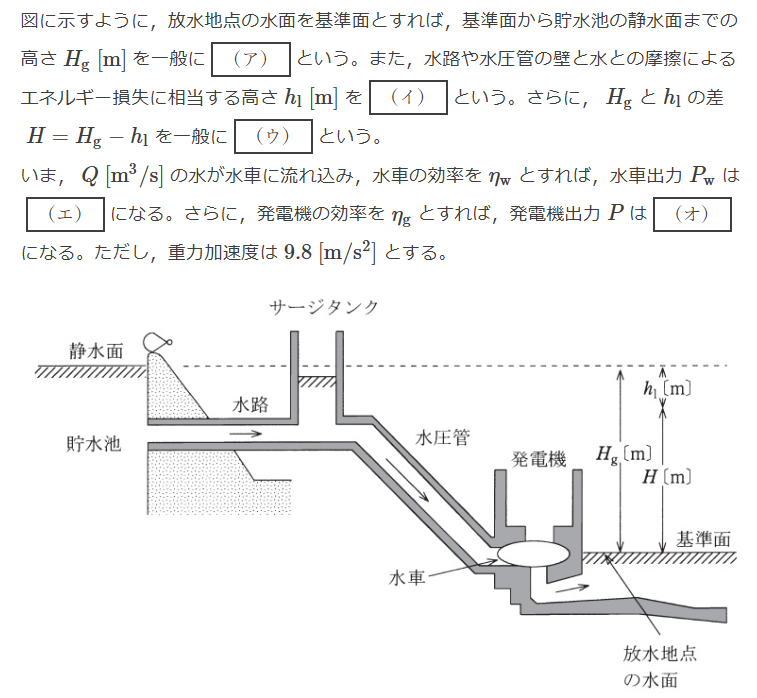 上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)〜(5)のうちから一つ選べ。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)〜(5)のうちから一つ選べ。

Ans.(3)
全揚程:ポンプ運転による全水頭$$H_P = H_G + H_1 + \frac{v_0^2}{2 g}$$ $$H_G:総落差、H_1:損失水頭の和、V_0:取水口における流速$$
揚水ポンプの電動機入力$$P_m = \frac{9.8 Q H_P}{\eta _P \eta _m}$$ $$\eta _P:揚水ポンプの効率、 \eta _m:電動機の効率$$
揚水所要発電量:$$V[m^3]を揚水するのに要する時間t[h]$$ $$W = P_m t = \frac{9.8 Q H_P}{\eta _P \eta _m} \frac{V}{3600 Q} = \frac{9.8 V H_P}{3600 \eta _P \eta _m} [kW h]$$

$$(a)電動機が要する電力 \frac{9.8 V H_P}{3600 \eta _P \eta _m}$$ $$= \frac{9.8 \times 1800000 \times 450}{3600 \times 09 \times 098}$$ $$= 2500000[kW・h]$$ $$(b)電動機入力P_m = \frac{9.8 Q H_P}{\eta _P \eta _m}$$ $$Q = \frac{P_m \eta _P \eta _m}{9.8 H_P}$$ $$ = \frac{300 \times 10^3 \times 0.9 \times 0.98}{9.8 \times 450} =60$$ $$Ans.(3)$$ $$$$
相似水車(落差1[m]のもと出力1[kW]発生する水車)の回転数
$$n_s = N \frac{P^\frac12}{H^\frac54}$$ $$H:有効落差[m],N:回転数[rpm],P:電気出力[kW]$$
無拘束速度
ある有効落差、開度、吸出高で運転中に発電機を急に無負荷にしたときの水車の上昇し得る最高速度
水撃作用
水車負荷の急激の減少により水車の流量が変動すると、水の流れの慣性のために水の持つ速度エネルギーが瞬間的な圧力上昇となり、水中でほぼ音速で移動し、水車ケーシングや水圧間の上昇又は下降が起こる。
対策:サージタンク又は上水槽の水位の変動により吸収・水圧管の強度を上げる。水車入口管の閉鎖時間を長くする。反動水車に制圧機、衝動水車にデフレクタを設ける。
キャビテーション
流水中のある点の圧力低下により、その部分の水が沸騰して水蒸気の泡ができ、それが壊れるときに金属面の壊食や振動を起こす現象。
対策:水の比速度を小さくする。吸出し菅の高さをあまり大きくしない。部分負荷運転を避ける。適切なランナ形状とし、表面仕上げを円滑にする。
速度調定率:回転速度の変化分と出力の変化分
$$R = \frac{\frac{N_1 - N_2}{N_n}}{\frac{P_2 - P_1}{P_n}}$$
$$P_n:定格出力、N_n:定格回転速度$$
$$N_1,P_1:変化前の速度と出力、N_2,P_2:変化後の速度と出力$$
速度変動率
速度の変化量と定格回転数の比
$$\delta = \frac{N_m - N_1}{N_n}$$
$$N_m:最大回転速度、N_1:負荷変化前の回転速度$$
揚水ポンプ水車の比速度
$$n_s = N \frac{\root \of Q}{H_p^\frac34}[m m^3/s]$$


Ans.(4)

Ans.(1)
水力発電/ 汽力発電/ 変電所/ 送電/ 原子力発電の仕組み
科学の部屋[工学・化学]