電験三種　法規　計算問題

需要設備の電力負荷

$$需要率＝\frac{最大需要電力}{需要設備の定格容量の合計}$$

$$不等率＝\frac{各負荷の最大需要電力の合計}{合成最大需要電力}$$合成最大需要電力：ある期間での最大需要電力。

１以上の値をとる。１の場合はすべての負荷の最大需要電力が同じ時間に提供される場合。

$$負荷率＝\frac{ある期間での平均需要電力}{ある期間での最大需要電力}$$

$$総合負荷率＝\frac{合成平均需要電力}{合成最大需要電力}$$

無効電力を減少させて力率を改善（cosθを１に近づける）させる。

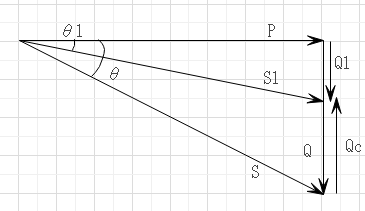
P：有効電力[W]、Q：無効電力[var]、S：皮相電力[VA]。cosθ：力率。

Qc：力率改善コンデンサによる無効電力。

S1：力率改善後の皮相電力、Q1：力率改善後の無効電力、cosθ1：力率改善後の力率

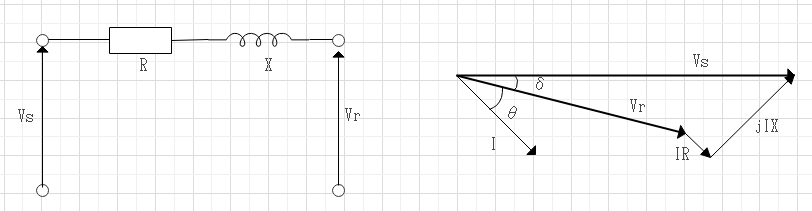
送電端の電圧Vsと受電端の電圧Vrの差

$$電圧降下（三相三線式）＝V_S - V_R \simeq \root \of 3 I (R\cos\theta + X \sin \theta )$$

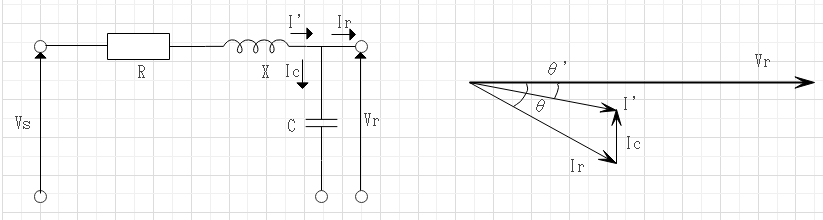
コンデンサを並列に接続すると力率が改善しリアクタンスに流れる電流が減るので電圧降下が軽減される。

$$電力損失（三相三線式）＝3I^2R$$

$$I=\root \of {I_p^2 + I_q^2}$$

$$I_p:抵抗に流れる電流、I_q:リアクタンスに流れる電流$$

コンデンサを並列に接続すると$$I_c：コンデンサに流れる電流$$

$$I=\root \of {I_p^2 + (I_q - I_c)^2}$$になるので電力損失が減る

P：有効電力[W]、Q：無効電力[var]、S：皮相電力[VA]。

$$S = \root \of {P^2 + Q~2}$$

コンデンサQcを接続すると

$$$S = \root \of {P^2 + (Q - Q_c)^2}$$

変圧器の鉄心中に発生する損失。負荷の大きさに関係なく一定。ヒステリシス損とうず電流損がある。

ヒステリシス損
ヒステリシスループ内の面積に相当する損失。$$P_h = \sigma _h f B_m^2 [W/kg]$$

うず電流損
磁束変化による鉄心内のうず電流によるジュール熱損。 $$P_e = \sigma _e (t f k_f B_m)^2 [W/kg]$$

$$\sigma _h,\sigma _e :材料による定数, f:周波数, B_m:最大磁束密度, t:鉄心の厚さ, k_f:波形率（\frac{実効値}{平均値}）$$

一次・二次側の巻線抵抗による損失。負荷電流の２乗に比例する。

$$P_c = K_m(I_1^2 r_1 + I_2^2) = K_m I_1^2(r_1 + r'_2)$$ $$K_m:定数,I_1,I_2:一次・二次側の電流,r_1,r_2:一次・二次側の抵抗,r'_2:一次側に変換した二次側の抵抗$$

$$\eta = \frac{P_{out}}{P_{out} + P_{loss}}×100[%]$$

$$\eta _d = \frac{一日中の供給電力量[kWh]}{一日中の供給電力量[kWh]＋一日中の損失電力量（鉄損＋銅損）[kWh]}×100$$効率が最大の時：銅損と鉄損が同じ