統計

統計の基礎知識

算術平均（相加平均） $$\overline x = \frac{x_1 + x_2 + … + x_n}{n} = \frac{\sum\limits^n _{i = 1} x_i}{n}$$

加重平均 $$\overline {x_W} = \frac{W_1x_1 + … + W_n x_n}{W_1 + … + W_n} W_i : 重み$$

幾何平均(相乗平均) $$m_g = \root n \of {\prod\limits^n _{i = 1} x_i }$$

分散 $$s^2 = \frac{\sum\limits^n _{i = 1} {(x_i - \overline x)^2}}{n}$$

標準偏差 $$s = \sqrt{\frac{\sum\limits^n _{i = 1} {(x_i - \overline x)^2}}{n}}$$

変動係数 $$c.v. = \frac{s}{\overline x}$$

最頻値（モード）

中央値（メジアン）

相関係数 $$r = \frac{\sum\limits^n _{i = 1} {(x_i - \overline x)^2 (y_i - \overline y)^2 }}{\sqrt{\sum\limits^n _{i = 1} {(x_i - \overline x)^2}}\sqrt{\sum\limits^n _{i = 1} {(y_i - \overline y)^2}}}$$ r>0:正の相関関係、r<0:負の相関関係

確率分布：統計量に対して想定されるさまざまな分布の総量

確率変数：理論的に確率で決まっている変数

生起確率：確率変数がとるそれぞれの値に対して起こりやすさ。合計は100％

正規分布

左右対称で平均値付近に集積するようなデータの分布を表した連続的な変数に関する確率分布

正規分布の確率密度関数 $$f(x) = \frac{1}{\root \of {2 \pi \sigma^2}} e^{- \frac{(x- \mu)^2}{2 \sigma^2}}$$ $$\mu = 0,\sigma^2 = 1の時の標準正規分布$$ $$f(x) = \frac{1}{\root \of {2 \pi }} e^{- \frac{x^2}{2 }}$$

ポアソン分布

所与の時間間隔で発生する離散的な事象を数える特定の確率変数xを持つ離散確率分布。単位時間当たりの生起確率 $$確率質量関数f(x) = \frac{e^{-\lambda} \lambda^x}{x!}$$ $$\lambda:所与の単位時間区間内で発生する事象の期待発生回数。試行回数n ×生起確率p$$ $$x:事象が所与の単位時間区間内に起こる回数$$

指数分布

事象の生起間隔（ある事象が起こって次にまた発生するまでの間隔。） $$f(x) = \lambda e^{-\lambda t}$$

χ²分布

標準化変量Zを二乗和したχ²値が従う確率分布で母分散の信頼区間の推定やクロス集計の検定に用いる。 $$\chi^2(n) = \frac{\sum\limits^n _{i = 1} {(x_i - \mu)^2}}{\sigma^2}$$$$ n:自由度、データの数$$

マルコフ過程

マルコフ性をもつ確率過程。未来の挙動が現在の値だけで決定され、過去の挙動と無関係

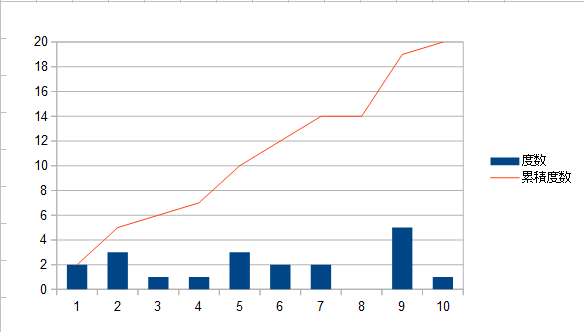
度数分布表

統計資料を階級に分け各階級ごとの度数を表の形式で表したもの

最小と最大値を探す

最大値と最小値の範囲をいくつか（階級数）に分ける。各区分の幅を階数幅

度数の欄にその回数に属するデータの個数を数えて記入

相対度数の欄には度数をパーセントで表す

累積度数の欄はその階級までの度数の合計を書く

累積相対度数の欄は累積度数欄の数値をパーセントで表す

代表値：データの特徴を要約して表す数値

平均値、最頻値、中央値

ばらつき

範囲（レンジ）：データの最大値−データの最小値

平均偏差：平均値からのずれの絶対値の平均

分散：偏差の２乗の平均

標準偏差：分散の平方根

変動係数：標準偏差を平均で割ったもの

回帰曲線：２組のデータの中心的な文武傾向を表す直線。最小二乗法によって求められる。 $$y = ax +b,f = \sum_i\{y_i - (ax_i+b)\}^2を最小$$ $$a = \frac{\sum\limits^n _{i = 1} {(x_i - \overline x)^2 (y_i - \overline y)^2 }}{\sum\limits^n _{i = 1} (x_i - \overline x)^2 }$$ $$b = \overline y - \frac{\sum\limits^n _{i = 1} {(x_i - \overline x)^2 (y_i - \overline y)^2 }}{\sum\limits^n _{i = 1} (x_i - \overline x)^2 } \bar x$$

決定係数（回帰直線の有効性）

$$R^2 = \frac{予測値の分散}{データの分散}$$

推定

現実の標本から母集団の未知の母数に対してその値や値の範囲を推定できるような信頼のおける命題を立てる

点推定：抽出集団データを用いて母集団の分布を表現するパラメータを点として推定。

$$推定平均値　\hat \mu = \frac{1}{n} \sum\limits^n_{i=1}x_i$$ $$推定標準偏差　\hat \sigma = \sqrt{\frac{\sum\limits^n _{i = 1} {(x_i - \hat \mu)^2}}{n-1}}$$

区間推定：点推定で推定したパラメータのばらつきや信頼区間を示すこと

$$標準誤差SE = \sqrt{\frac{N-n}{N}} \frac{\hat \sigma}{\sqrt{n}}$$ $$N:母集団の要素数、n：抽出した標本数$$ $$N \ll 1 ,SE=\frac{\hat \sigma}{\sqrt{n}}$$

信頼区間：母数がどのような数値の範囲にあるか確率的に示す方法

検定

あらかじめ母集団の性質と母数の値を仮定して現実に観測されたデータが果たしてこの母集団から抽出された標本とみなせるのかどうかを推論する

仮説検定
問題を設定する
帰無仮説と対立仮説を設定する
優位水準と検出力を決める
母集団がら標本集団を無作為抽出する
標本集団のデータを測定して要約値を求める
帰無仮説が正しいと仮定したときの標本平均の分布と対立仮説が正しいと仮定したときの標本平均の分布を描く
標本平均の分布における棄却域を求める
標本平均が棄却域に入っているかどうかを調べる
標本平均が棄却域に入っている時、帰無仮説を否定した仮定を統計学的結論として採用
標本平均が棄却域に入ってない時、対立仮説を否定して仮説を統計学的結論として利用
統計学的結論を科学的に評価して実質科学的結論を下す