数値計算:離散数学を用いて様々な手法による近似計算により解を求めること
ニュートン法
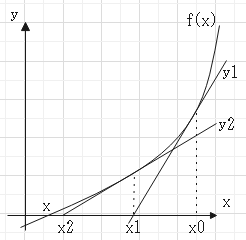
反復法による求根アルゴリズム
・予想される真の解に近いと思われる値をとる
・そこでグラフの接線を考え、x切片を計算
・そこで接線を考え…の繰り返し
$$y_1 = f'(x_0)(x-x_0)+f(x_0)…x_1 = x_0-\frac{f(x_0)}{f'(x_0)}$$
オイラー法
微分方程式の数値解析の一つ
$$\frac{dy}{dx} = f(x,y),(y(x_0)=y_0)$$
$$初期値x_0,y_0(=f(x_0))を求める$$
$$y_1 = y(x_1)=y(x_0+h)=y(x_0);h f(x_0,y_0) = y_0 + h f(x_0,y_0)$$
$$y_2 = y(x_2)=y(x_1+h)=y(x_1);h f(x_1,y_1) = y_1 + h f(x_1,y_1)$$
$$順次y_3…y_kを計算$$
$$\frac{dy}{dx} = f(x,y)=lim_{h \rightarrow 0}\frac{y(x+h)-y(x)}{h}\simeq \frac{y(x+h)-y(x)}{h}$$
$$$$
ルンゲ・クッタ法
微分方程式・数値解析の一つ。オイラー法より高精度 $$\frac{dy}{dx} = f(x,y),x_{n+1}=x_n+h,y_{n+1}=y_n+k$$
$$y_{n+1}=y_n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)$$
$$k_1 = h f(x_n,y_n)$$
$$k_2 = h f(x_n+\frac{h}{2},y_n+\frac{k_1}{2})$$
$$k_3 = h f(x_n+\frac{h}{2},y_n+\frac{k_2}{2})$$
$$k_4 = h f(x_n+h,y_n+k_3)$$
数値微分(差分法)
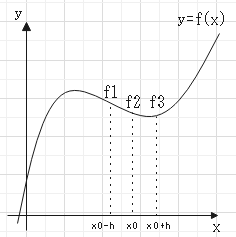
前進差分$$f'(x_0) = \frac{f_3 - f_2}{h} = \frac{f(x_0 + h) - f(x_0)}{h}$$
後進差分$$f'(x_0) = \frac{f_2 - f_1}{h} = \frac{ f(x_0) - f(x_0 - h)}{h}$$
中央差分$$f'(x_0) = \frac{f_3 - f_1}{h} = \frac{f(x_0 + h) - f(x_0 - h)}{2h}$$
数値積分(台形法)
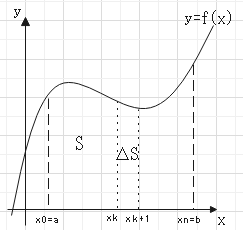
$$\Delta S = \int^{x_{k+1}}_{x_k}f(x)dx \simeq \frac{f(x_k)+f(x_{k+1})}{2}(x_{k+1}-x_k) = \frac{b-a}{n}\frac{f(x_k)+f(x_k+1)}{2}$$
$$S = \sum_{k=0}^{n-1}\Delta S = \frac{b-a}{n}\{f(x_0)+2(f(x_1)+…+f(x_{n-1})+f(x_n))\}$$
シンプソン法
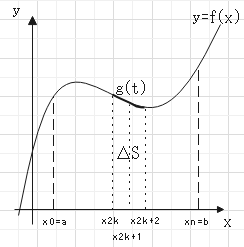
三点を通る2次曲線で補間$$g(t) = p +qt +rt^2$$
$$\Delta S = \int^{x_{2k+2}}_{x_{2k}}f(x)dx = \int^h_{-h}g(t)dt = \int^h_{-h}(p+qt+rt^2)dt$$
$$f(x_{2k}) = g(-h) = p-qh-rh^2$$
$$f(x_{2k+1})=g(0)=p$$
$$f(x_{2k+2})=g(h)=p+qh+rh^2$$
$$\Delta s = \frac{b-a}{2n}\frac{f(x_{2k})+4f(x_{2k+1})+f(x_{2k+2})}{3}$$
$$S = \sum^{n-1}_{k=0}\Delta S\\ = \frac{b-a}{6n}\{f(x_0)+4(f(x_{1})+f(x_{3})+…+f(x_{2n-1}))+…+2(f(x_2)+f(x_4)+…+f(x_{2n-2})+f(x_{2n}))\}$$